Честное разбиение множества S на k разбиений

Question

Существует множество S, содержащее N целых чисел, каждое со значением 1<=X<=10^6. Проблема состоит в том, чтобы разбить множество S на k разделов. Значение раздела - это сумма элементов, присутствующих в нем. Разделение должно быть выполнено таким образом, чтобы общее значение множества S было справедливо распределено между k разделами. Также необходимо определить математическое значение справедливости (например, цель может состоять в том, чтобы минимизировать стандартное отклонение значений разделов от среднего значения набора S (то есть суммы (S)/k))

например, S = {10, 15, 12, 13, 30, 5}, k=3

Хорошее разбиение будет {30}, {10, 15}, {12, 13, 5}

Неверное разбиение будет {30, 5}, {10, 15}, {12, 13}

Первый вопрос - математически выразить условие, чтобы один раздел был лучше другого. Второй вопрос - как решить проблему. Проблема в NP-Hard. Есть ли эвристика?

В задаче, которую я пытаюсь решить, N <= (k*logX)^2 и K варьируется от 2 до 7.

================================================== ================================

Основываясь на других связанных вопросах SO, есть две разумные функции для оценки распределения:

а) Минимизировать значение раздела с максимальным значением.

Во-вторых, это не очень хорошая метрика. Рассмотрим набор {100, 40, 40}, который нужно разделить на три подмножества. Этот показатель не различает следующие два распределения, хотя одно явно лучше другого.

Распределение 1: {100}, {40}, {40} и Распределение 2: {100}, {40, 40}, {}

б) Минимизировать максимум разности любых двух значений в данном разделе, т. е. минимизировать максимум |AB| для любого А, Б

Answer 1

Я думаю, что хороший показатель будет:

let the result set be s1,s2,...,sk
let MAX be max{sum(si) for each i}
f({s1,...,sk}) = Sigma(MAX-sum(si)) for each i)

положительный момент: идеальное распределение даст всегда 0!
недостаток: если нет идеального решения, лучший результат не даст 0.

жадный эвристик для этой проблемы будет:

sorted<-sort(S) (let's say sorted[0] is the highest)
s1=s2=...=sk= {}
for each x in sorted:
   s <- find_min() (*)
   s.add(x)

где find_min() возвращает s такой, что sum(s) <= sum(si) для каждого si.

это решение даст f (метрики, определенные выше) так, что f(sol) <= (k-1)*max{S} (отсюда это доказательство этой границы):

утверждение: для каждого подмножества, MAX- sum(s) <= max{S}
доказательство - по индукции: на каждом этапе претензия верна для временного решения.
на каждом шаге пусть MAX будет max{sum(si)} в начале итерации (до добавления)!

base: the set of subsets at start is {},{},.. MAX=sum(si)=0 for each si. 
step: assume the assumption is true for iteration i, we'll show it is also true for iteration i+1:
let s be the set that x was added to, then MAX-sum(s) <= max{S} (induction assumption).
if sum(s) + x <= MAX: we are done, MAX was not changed.
else: we sorted the elements at start, so x <= max{S}, and thus if s was chosen
   (sum(si) >= sum(s) for each si) and sum(s) + x > MAX then: for each si, sum(si) + x >=
   sum(s) + x, so sum(s)+x - sum(si) <= x <= max{S}. since sum(s)+x will be the MAX next 
   iteration, we are done.

потому что для каждого набора MAX-sum(si) <= max{S} (и, очевидно, для максимального набора, MAX-sum(si)=0), в целом Sigma(MAX-sum(si)) <= (k-1)*max{S}, как и было обещано.

РЕДАКТИРОВАТЬ:
У меня было немного свободного времени, поэтому я запрограммировал обе эвристики, предложенные мной и @Akhil, и обе метрики, во-первых, оба результата являются убедительными (согласно парному t-критерию Уилкоксона), но, что лучше, определяется Какую метрику вы выберете, к удивлению, алгоритм, который пытался минимизировать f() (@Akhil`s), набрал меньше баллов для этого же f, но выше для второй метрики.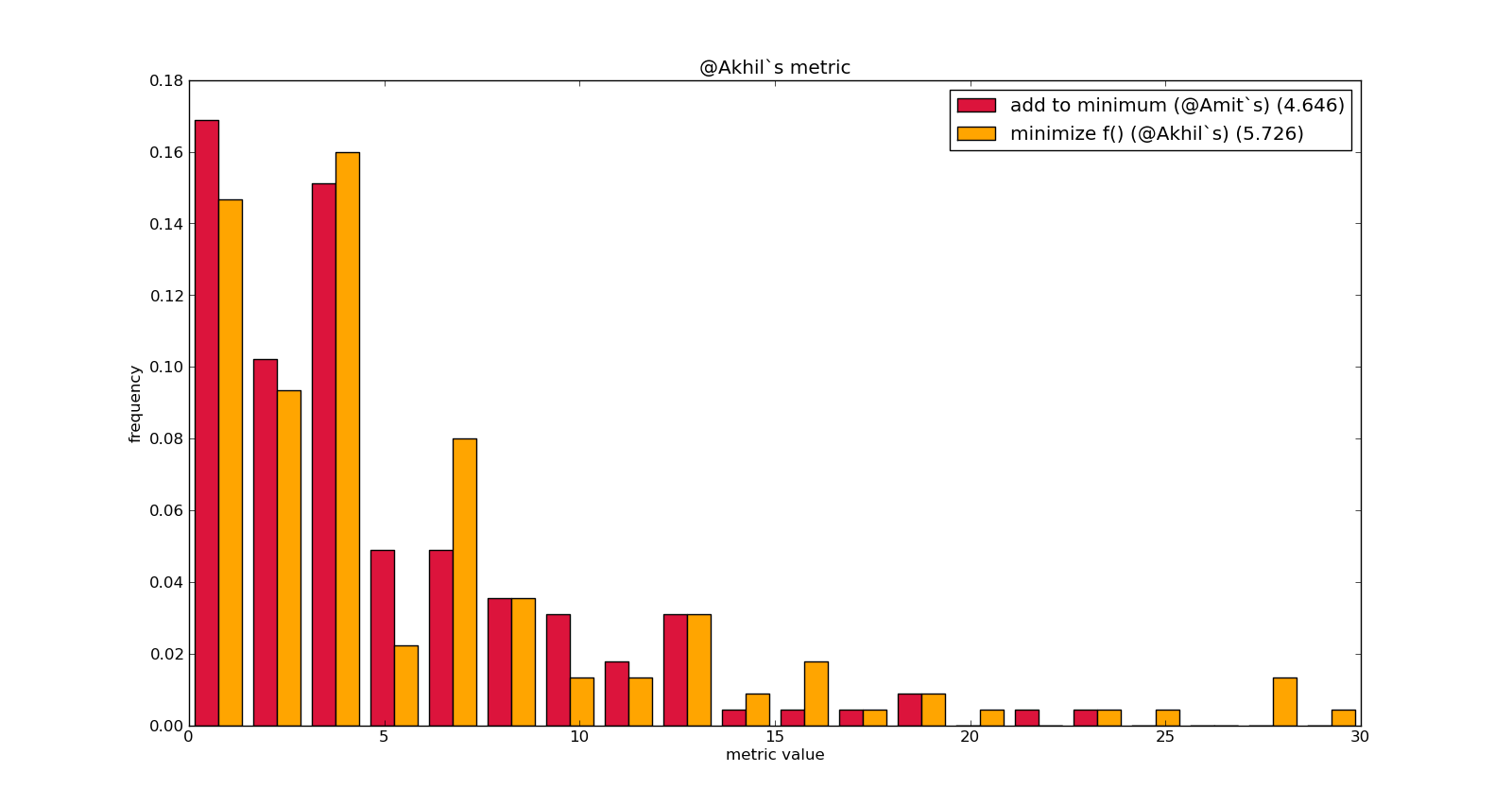

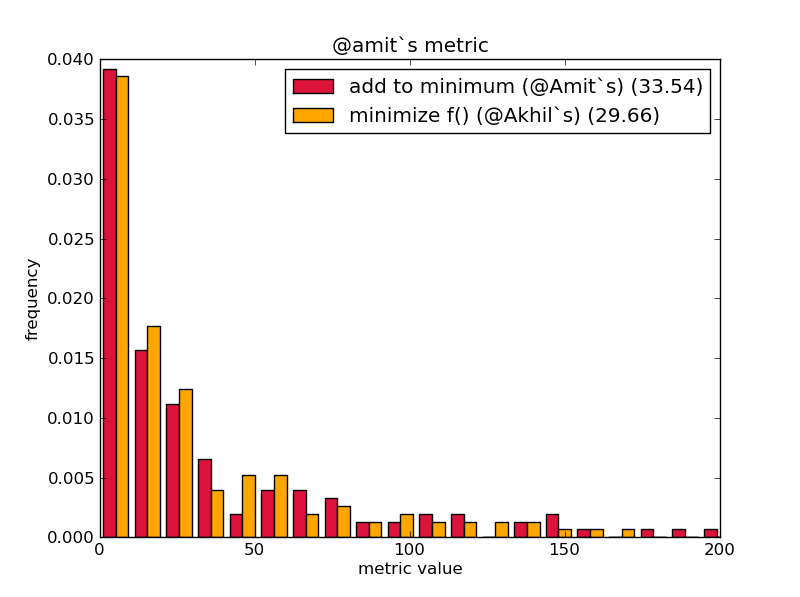
Answer 2

Одним из эвристических подходов было бы распределение больших весов между сумками как можно более равномерно, оставляя достаточно меньшие веса, чтобы у вас осталась подзадача с большим количеством степеней свободы. Повторите в подпроблемах при необходимости. Эта эвристика предполагает, что ваше распределение не слишком геометрическое, например {1000} and {100, 10, 1}, и слегка предполагает, что ваша штрафная функция будет штрафовать ноль-назначения или очень большие выбросы.

Например:

distributeFairly(numbers, bins):
    distributeFairlySubproblem(numbers, bins):
        n = len(numbers)
        numElementsToDefer = min(-n//3,20*k)  # modify as appropriate, e.g. to avoid len(toPlace)<len(toDefer)

        toDefer = numbers[-numElementsToDefer:]
        toPlace = numbers[:-numElementsToDefer]

        newBins = shoveThemIn(toPlace, copy(bins))
        return distributeFairlySubproblem(toDefer, newBins)

    initialGuess = distributeFairlySubproblem(sorted(numbers,reverse=True), [[]]*k)
    return anneal(initialGuess)

Answer 3

Пусть метрика минимизирует max(sum(si) - sum(sj)), где si и sj - любые два подмножества в результирующем разбиении множества S.

Допустим, у нас есть распределение D, и нам нужно включить другой элемент x в распределение D. Добавьте его к подмножеству s так, чтобы указанная выше метрика была минимизирована.

Не удалось доказать никаких границ, но интуиция говорит, что это даст хорошее приближение к оптимальному? Кто-нибудь хорошо доказывает границы?