Проверка маршрута ориентированного графа в ASP

Question

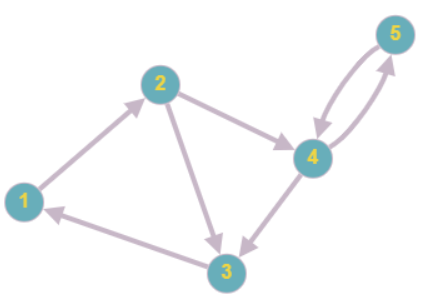
Для многонаправленного графа ниже я пытаюсь написать программу, которая посещает все ребра хотя бы один раз. Например, на приведенном ниже графике я ищу результат, похожий на «край (1,2), край (2,3), край (3,1), край (1,2), край (2,4) , край(4,5), край(5,4), край(4,3), край(3,1)"

Вот мой код до сих пор. Он не работает должным образом, но я не знаю, как это исправить. Не могли бы вы помочь, как продолжить? Любые советы или код приветствуются.

По сути, я считаю, что ищу вариант эйлерова цикла, в котором ребра можно посещать более одного раза.

      edge(1,2). edge(2,3). edge(3,1).
edge(2,4). edge(4,3).
edge(4,5). edge(5,4).
    
#const s=1.
start(s).

time(1..20). % allow at most 20 time-steps

1 { move(edge(X,Y),step(T)) : edge(X,Y) } 1 :- time(T).

:- move(edge(X,Y),step(1)), edge(X,Y), X!=s. % start from s

:- move(edge(X,Y_1),step(T)), move(edge(Y_2,Y),step(TT)), TT=T+1, Y_1!=Y_2.

visited(X,Y,T) :- time(T),move(edge(X,Y),step(S)), S<T, T<=20.
visited(X,Y,T) :- time(T),move(edge(Y,X),step(S)), S<T, T<=20.

:- edge(X,Y), not visited(X,Y,20).

:- move(edge(X,Y),step(S)), S<=20, Y!=s. %ensures path is cycle (back to s)

#minimize { T : time(T) }. % here i try to get as many steps as possible out of the upper bound of 20 

#show move/2.

Answer 1

В вашем коде есть проблема в строке

      1 { move(edge(X,Y),step(T)) : edge(X,Y) } 1 :- time(T).

Проблема здесь в том, что вы заставляете двигаться на каждом временном шаге, а это означает, что ваш путь должен состоять из 20 шагов, что может быть проблематичным для проблемных экземпляров, где нет решения ровно для 20 шагов.

Кроме того, ваша линия

      :- move(edge(X,Y),step(S)), S<=20, Y!=s.

является проблемой, поскольку заставляет каждое движение заканчиваться s- следовательно, код невыполним.

Также вы ищете минимум или максимум? Ваш код указывает минимум, ваш комментарий говорит максимум.

Я немного изменил ваш код, и теперь он работает. Основное изменение состоит в том, чтобы ввести количество пройденных шагов и убрать таймер из предиката. visited.

      #const s=1.
start(s).
1 {endt(1..20)} 1. % guess end time
time(1..T) :- endt(T). 

1 { move(edge(X,Y),step(T)) : edge(X,Y) } 1 :- time(T).

:- move(edge(X,Y),step(1)), edge(X,Y), X!=S, start(S). % start from s
:- move(edge(X,Y_1),step(T)), move(edge(Y_2,Y),step(T+1)), Y_1!=Y_2.
:- move(edge(X,Y),step(S)), edge(X,Y), Y!=s, endt(S). % end from s

visited(X,Y) :- move(edge(X,Y),step(_)).
visited(X,Y) :- move(edge(Y,X),step(_)).

:- edge(X,Y), not visited(X,Y). % visit all edges

#minimize { T : endt(T) }. 
#show move/2.

Выход:

      Answer: 1
move(edge(1,2),step(1)) move(edge(2,3),step(2)) move(edge(3,1),step(3)) move(edge(1,2),step(4)) move(edge(2,4),step(5)) move(edge(4,5),step(6)) move(edge(5,4),step(7)) move(edge(4,3),step(8)) move(edge(3,1),step(9))
Optimization: 9
OPTIMUM FOUND

за #maximize { T : endt(T) }.:

      Answer: 1
move(edge(1,2),step(1)) move(edge(2,3),step(2)) move(edge(3,1),step(3)) move(edge(1,2),step(4)) move(edge(2,4),step(5)) move(edge(4,5),step(6)) move(edge(5,4),step(7)) move(edge(4,3),step(8)) move(edge(3,1),step(9))
Optimization: -9
Answer: 2
move(edge(1,2),step(1)) move(edge(2,3),step(2)) move(edge(3,1),step(3)) move(edge(1,2),step(4)) move(edge(2,4),step(5)) move(edge(4,5),step(6)) move(edge(5,4),step(7)) move(edge(4,5),step(8)) move(edge(5,4),step(9)) move(edge(4,5),step(10)) move(edge(5,4),step(11)) move(edge(4,5),step(12)) move(edge(5,4),step(13)) move(edge(4,5),step(14)) move(edge(5,4),step(15)) move(edge(4,3),step(16)) move(edge(3,1),step(17)) move(edge(1,2),step(18)) move(edge(2,3),step(19)) move(edge(3,1),step(20))
Optimization: -20