частичное разложение Таккера тензорно

Question

Я хочу применить алгоритм частичной разложения tucker, чтобы минимизировать набор данных тензора изображений MNIST (60000,28,28), чтобы сохранить его функции при последующем применении другого машинного алгоритма, такого как SVM. У меня есть этот код, который минимизирует второе и третье измерения тензора

      i = 16
j = 10
core, factors = partial_tucker(train_data_mnist, modes=[1,2],tol=10e-5, rank=[i,j])
train_datapartial_tucker = tl.tenalg.multi_mode_dot(train_data_mnist, factors, 
                              modes=modes, transpose=True)
test_data_partial_tucker = tl.tenalg.multi_mode_dot(test_data_mnist, factors, 
                              modes=modes, transpose=True)

Мой вопрос в том, как найти лучший ранг [i, j], когда я использую partial_tucker в тензорном режиме, что даст наилучшее уменьшение размеров изображения при сохранении как можно большего количества данных, потому что я не нашел в нем этого. Благодарность

Answer 1

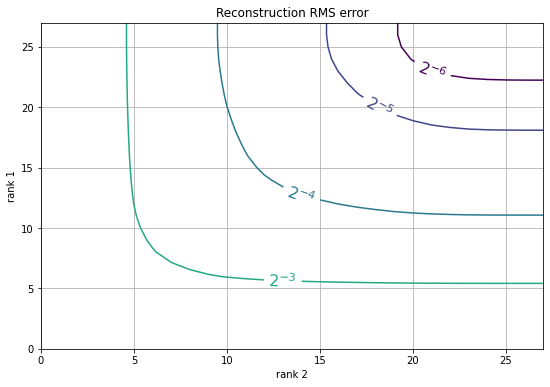
Точно так же, как анализ главных компонентов, частичное разложение Такера будет давать лучшие результаты по мере увеличения ранга в том смысле, что оптимальный среднеквадратический остаток реконструкции будет меньше.

В общем, функции (тензор), которые позволяют точно реконструировать исходные данные, могут быть использованы для подобных прогнозов (для любой модели мы можем предварительно выполнить преобразование, которое реконструирует исходные данные из исходных данных). coreОсобенности).

      import mxnet as mx
import numpy as np
import tensorly as tl
import matplotlib.pyplot as plt
import tensorly.decomposition

# Load data
mnist = mx.test_utils.get_mnist()
train_data = mnist['train_data'][:,0]


err = np.zeros([28,28]) # here I will save the errors for each rank
batch = train_data[::100] # process only 1% of the data to go faster
for i in range(1,28):
  for j in range(1,28):
    if err[i,j] == 0:
      # Decompose the data
      core, factors = tl.decomposition.partial_tucker(
                        batch, modes=[1,2], tol=10e-5, rank=[i,j])
      # Reconstruct data from features
      c = tl.tenalg.multi_mode_dot(core, factors, modes=[1,2]);
      # Calculate the RMS error and save
      err[i,j] = np.sqrt(np.mean((c - batch)**2));

# Plot the statistics
plt.figure(figsize=(9,6))
CS = plt.contour(np.log2(err), levels=np.arange(-6, 0));
plt.clabel(CS, CS.levels, inline=True, fmt='$2^{%d}$', fontsize=16)
plt.xlabel('rank 2')
plt.ylabel('rank 1')
plt.grid()
plt.title('Reconstruction RMS error');

Обычно у вас лучший результат при сбалансированном ранге, т.е. iа также jне сильно отличаются друг от друга.

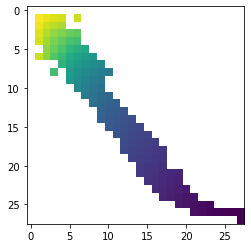
По мере увеличения ошибки мы можем улучшить сжатие, мы можем ранжировать (i,j)по ошибке и строить только там, где ошибка минимальна для данного размера объекта i * j, как это

      X = np.zeros([28, 28])
X[...] = np.nan;
p = 28 * 28;
for e,i,j in sorted([(err[i,j], i, j) for i in range(1, 28) for j in range(1, 28)]):
  if p < i * j:
    # we can achieve this error with some better compression
    pass
  else:
    p = i * j;
    X[i,j] = e;
plt.imshow(X)

Везде в белом регионе вы тратите ресурсы, выбор

Answer 2

Итак, если вы посмотрите на исходный код для tensorlyсвязанный здесь , вы можете видеть, что документация для рассматриваемой функции partial_tuckerговорит:

      """
Partial tucker decomposition via Higher Order Orthogonal Iteration (HOI)
Decomposes 'tensor' into a Tucker decomposition exclusively along 
the provided modes.

Parameters
----------
tensor: ndarray
modes: int list
list of the modes on which to perform the decomposition
rank: None, int or int list
size of the core tensor, 
if int, the same rank is used for all modes
"""

Цель этой функции состоит в том, чтобы предоставить вам аппроксимацию, которая сохраняет как можно больше данных для данного ранга . Я не могу указать вам, какой ранг «даст наилучшее уменьшение размерности изображения при сохранении как можно большего количества данных», потому что оптимальный компромисс между уменьшением размерности и потерей точности — это то, что не имеет объективно «правильного», абстрактного ответа, поскольку это будет во многом зависеть от конкретных целей вашего проекта и вычислительных ресурсов, доступных вам для достижения этих целей.

Если бы я сказал вам сделать «лучший ранг», это в первую очередь устранило бы цель этой приблизительной декомпозиции, потому что «лучший ранг» будет рангом, который не дает «потери», который больше не является приближением к фиксированной величине. ранг и вид переводит термин приближениебессмысленный. Но как далеко можно отклониться от этого «наилучшего ранга», чтобы получить уменьшение размерности, — это не тот вопрос, на который кто-либо другой может дать вам объективный ответ. Конечно, можно было бы высказать свое мнение, но это мнение будет зависеть от гораздо большего количества информации, чем я имею от вас на данный момент. Если вы ищете более глубокое представление об этом компромиссе и о том, какой компромисс подходит вам лучше всего, я бы предложил опубликовать вопрос с более подробной информацией о вашей ситуации на сайте в сети стека, более ориентированном на математические/статистические основы размерности. сокращения и в меньшей степени на аспектах программирования, на которых больше внимания сосредоточено Stack Overflow, таких как Stack Exhange Cross Validated или, возможно, Stack Exhange Data Science.

Источники/Ссылки/Дополнительная литература:

1. Блог/Статья о разложениях Такера
2. «Некоторые математические заметки по трехрежимному факторному анализу» - Статья Ледьярда Р. Такера о разложении Такера.
3. «Многолинейное разложение по сингулярным значениям» Латаувера и др.
4. «О наилучшей ранговой 1 и ранговой (R1,R2,...,RN) аппроксимации тензоров высшего порядка» Латаувера и др.