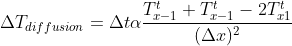Смоделируйте температуру вдоль трубы с движущейся водой с помощью deSolve и ReacTran

Question

Я моделирую кольцевую трубку с текущей водой и температурным градиентом, используя deSolve::ode(). Кольцо моделируется как вектор, в котором каждый элемент имеет значение температуры и положение.

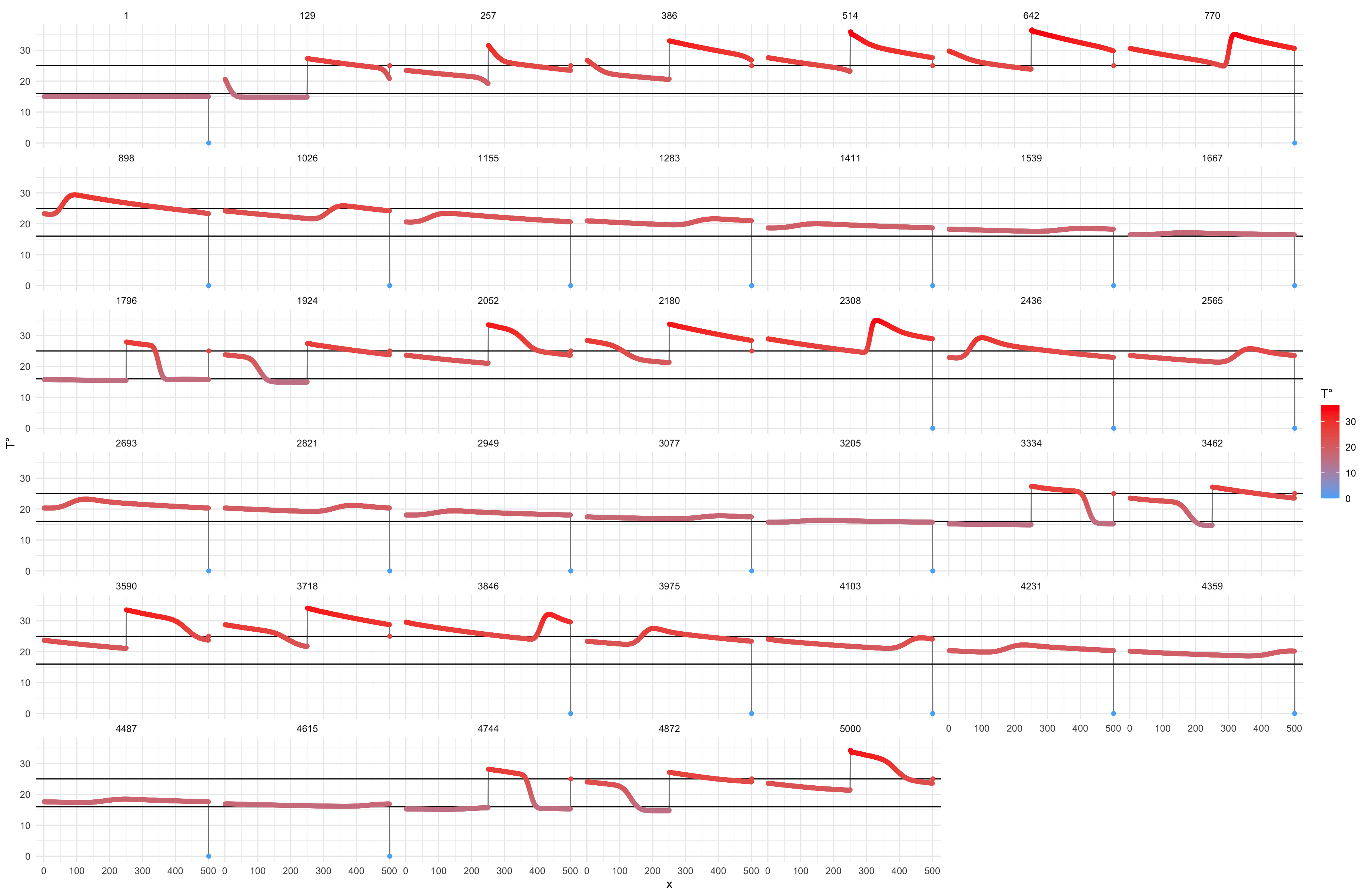
Я моделирую распространение тепла через:

Которая использует локальную кривизну температуры для определения временного градиента.

Как предлагается здесь deSolve: дифференциальные уравнения с двумя последовательными динамиками , я использую ReacTranчтобы обратиться к движению воды, но меня смущает параметризация.
В качестве первой попытки я попробовал:

      ReacTran::advection.1D(v, v = vel, dx = 1, C.up = v[L], C.down = v[1], adv.method = 'Up')$dC

моделирование температуры как концентрации растворенного вещества. Здесь v представляет собой трубу, разделенную на L сегменты с температурой v[i]. Распространяется со скоростью vel который определяется с точки зрения dxза временной шаг (я не уверен на 100% в этом, поэтому +1, если кто-то может это прокомментировать). Я принимаю возвращенный dC (дельта концентрации) как эквивалент изменения температуры dT за временной шаг.

В конце концов, dT из-за диффузии тепла суммируется с движением тепла при определении общего изменения температуры вдоль каждого сегмента трубы.

Я хотел бы знать, верен ли мой подход, а именно:

• Можно ли использовать адвекцию.1D() для моделирования температурного потока, поскольку это была концентрация?
• Правильно ли просто добавить dT из-за диффузии тепла к тому, что связано с движением воды, то есть являются двумя добавками?

Детали модели:

В моей модели есть несколько источников изменения температуры: спонтанная симметричная диффузия тепла; поток воды; источник тепла, который включается, если температура рядом с датчиком (помещенным перед источником тепла) падает ниже нижнего порога, и отключается, если поднимается выше верхнего порога; постоянное рассеивание тепла, определяемое циклической внешней температурой.

В plot_type Аргумент позволяет визуализировать либо временную последовательность температуры в водяной трубе («трубе»), либо температурную последовательность на датчиках (до и после нагревателя).

      library(deSolve)
library(dplyr)
library(ggplot2)
library(tidyr)
library(ReacTran)

test <- function(simTime = 5000, vel = 1, L = 500, thresh = c(16, 25), heatT = 25,
                                    heatDisp = .0025,   baseTemp = 15, alpha = .025,
                                    adv_method = 'up', plot_type = c('pipe', 'sensors')) {
    
    plot_type <- match.arg(plot_type)

    thresh <- c(16, 25)

    sensorP <- round(L/2)

    vec <- c(rep(baseTemp, L), 0)

    eventfun <- function(t, y, pars) {

        heat <- y[L + 1] > 0

        if (y[sensorP] < thresh[1] & heat == FALSE) { # if heat is FALSE -> T was above the threshold
            #browser()
            y[L + 1] <- heatT
        }

        if (y[sensorP] > thresh[2] & heat == TRUE) { # if heat is TRUE -> T was below the threshold
            #browser()
            y[L + 1] <- 0
        }

        return(y)
    }

    rootfun <- function (t, y, pars) {

        heat <- y[L + 1] > 0

        trigger_root <- 1

        if (y[sensorP] < thresh[1] & heat == FALSE & t > 1) { # if heat is FALSE -> T was above the threshold

            trigger_root <- 0
        }

        if (y[sensorP] > thresh[2] & heat == TRUE & t > 1) { # if heat is TRUE -> T was below the threshold

            trigger_root <- 0
        }


        return(trigger_root)
    }

    roll <- function(x, n) {
        x[((1:length(x)) - (n + 1)) %% length(x) + 1]
    }

    fun <- function(t, y, pars) {

        v <- y[1:L]

        # Heat diffusion: dT/dt = alpha * d2T/d2X
        d2Td2X <- c(v[2:L], v[1]) + c(v[L], v[1:(L - 1)]) - 2 * v

        dT_diff <- pars * d2Td2X

        # Moving water
        dT_flow <- advection.1D(v, v = vel, dx = 1, C.up = v[L], C.down = v[1],
                                                        adv.method = adv_method)$dC

        dT <- dT_flow + dT_diff

        # heating of the ring after the sensor
        dT[sensorP + 1] <- dT[sensorP  + 1] + y[L + 1]

        # heat dispersion based on cycling ambient temperature
        dT <- dT - heatDisp * (v - baseTemp + 2.5 * sin(t/(60*24) * pi * 2))

        return(list(c(dT, 0)))
    }

    out <- ode.1D(y = vec, times = 1:simTime, func = fun, parms = alpha, nspec = 1,
                                    events = list(func = eventfun, root = T),
                                    rootfunc = rootfun)


    if (plot_type == 'sensors') {

        ## Trend of the temperature at the sensors levels
        out %>%
            {.[,c(1, sensorP + 1, sensorP + 3, L + 2)]} %>%
            as.data.frame() %>%
            setNames(c('time', 'pre', 'post', 'heat')) %>%
            mutate(Amb = baseTemp + 2.5 * sin(time/(60*24) * pi * 2)) %>%
            pivot_longer(-time, values_to = "val", names_to = "trend") %>%
            ggplot(aes(time, val)) +
            geom_hline(yintercept = thresh) +
            geom_line(aes(color = trend)) +
            theme_minimal() +
            theme(panel.spacing=unit(0, "lines")) +
            labs(x = 'time', y = 'T°', color = 'sensor')
    } else {

    ## Trend of the temperature in the whole pipe
    out %>%
        as.data.frame() %>%
        pivot_longer(-time, values_to = "val", names_to = "x") %>%
        filter(time %in% round(seq.int(1, simTime, length.out = 40))) %>%
        ggplot(aes(as.numeric(x), val)) +
        geom_hline(yintercept = thresh) +
        geom_line(alpha = .5, show.legend = FALSE) +
        geom_point(aes(color = val)) +
        scale_color_gradient(low = "#56B1F7", high = "red") +
        facet_wrap(~ time) +
        theme_minimal() +
        theme(panel.spacing=unit(0, "lines")) +
        labs(x = 'x', y = 'T°', color = 'T°')
    }
}

Вот график модели на 500 сотен временных точек. Последняя точка каждого подзаголовка показывает, включен или выключен обогрев, и его температуру; две горизонтальные линии определяют температурные пороги включения / выключения обогрева. Тенденция во времени / пространстве кажется реалистичной, но я не уверен, имеет ли она физический смысл.