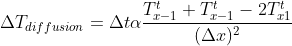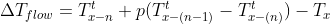deSolve: дифференциальные уравнения с двумя последовательными динамиками
Я моделирую кольцевую трубку с текущей водой и температурным градиентом, используя
deSolve::ode(). Кольцо моделируется как вектор, в котором каждый элемент имеет значение температуры и положение.
Я моделирую формулу рассеивания тепла:
Но я также борюсь с перемещением воды по кольцу. Теоретически это просто замена температуры в элементе i в векторе трубки на температуру в месте элемента s ранее. Поскольку s не может быть целым числом, его можно разделить на целую часть ( n ) и дробную часть ( p ): s=n+ p . Следовательно, изменение температуры из-за движения воды становится:
Проблема в том, что s равно скорости воды v на dt, вычисляемое на каждой итерации решателя од.
Моя идея состоит в том, чтобы рассматривать явления как аддитивные, то есть сначала вычислять (1), затем (2) и, наконец, складывать их вместе. Но я боюсь эффекта времени. Решатель од с неявными методами автоматически определяет временной шаг и линейно уменьшает единичную дельту изменения.
Мой вопрос в том, правильно ли просто возвращать (1) + (2) в производной функции, или я должен разбить два процесса и вычислить производные отдельно. Во втором случае, каким будет предложенный подход?
РЕДАКТИРОВАТЬ: по предложению @tpetzoldt я попытался реализовать поток воды, используя. В моей модели есть несколько источников изменения температуры: спонтанная симметричная диффузия тепла; поток воды; источник тепла, который включается, если температура рядом с датчиком (помещенным перед источником тепла) падает ниже нижнего порога, и отключается, если поднимается выше верхнего порога; постоянное рассеивание тепла, определяемое циклической внешней температурой.
Под разделом «Движущаяся вода» все еще находится моя предыдущая версия кода, теперь замененная на. В
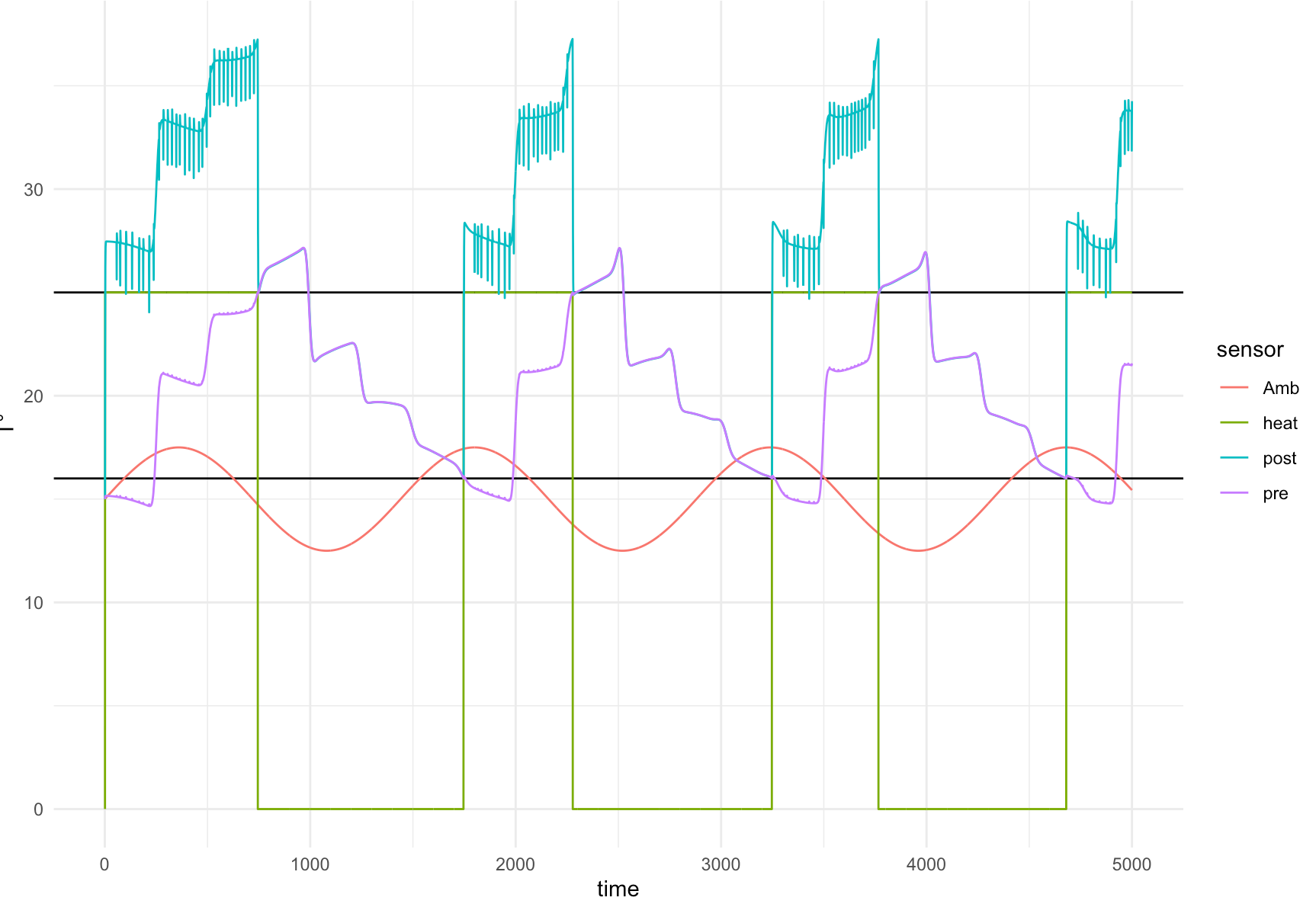
plot_type Аргумент позволяет визуализировать либо временную последовательность температуры в водяной трубе («трубе»), либо последовательность температур на датчиках (до и после нагревателя).
test <- function(simTime = 5000, vel = 1, L = 500, thresh = c(16, 25), heatT = 25,
heatDisp = .0025, baseTemp = 15, alpha = .025,
adv_method = 'up', plot_type = c('pipe', 'sensors')) {
library(deSolve)
library(dplyr)
library(ggplot2)
library(tidyr)
plot_type <- match.arg(plot_type)
thresh <- c(16, 25)
sensorP <- round(L/2)
vec <- c(rep(baseTemp, L), 0)
eventfun <- function(t, y, pars) {
heat <- y[L + 1] > 0
if (y[sensorP] < thresh[1] & heat == F) { # if heat is FALSE -> T was above the threshold
#browser()
y[L + 1] <- heatT
}
if (y[sensorP] > thresh[2] & heat == T) { # if heat is TRUE -> T was below the threshold
#browser()
y[L + 1] <- 0
}
return(y)
}
rootfun <- function (t, y, pars) {
heat <- y[L + 1] > 0
trigger_root <- 1
if (y[sensorP] < thresh[1] & heat == F & t > 1) { # if heat is FALSE -> T was above the threshold
#browser()
trigger_root <- 0
}
if (y[sensorP] > thresh[2] & heat == T & t > 1) { # if heat is TRUE -> T was below the threshold
#browser()
trigger_root <- 0
}
return(trigger_root)
}
roll <- function(x, n) {
x[((1:length(x)) - (n + 1)) %% length(x) + 1]
}
fun <- function(t, y, pars) {
v <- y[1:L]
# Heat diffusion: dT/dt = alpha * d2T/d2X
d2Td2X <- c(v[2:L], v[1]) + c(v[L], v[1:(L - 1)]) - 2 * v
dT_diff <- pars * d2Td2X
# Moving water
# nS <- floor(vel)
# pS <- vel - nS
#
# v_shifted <- roll(v, nS)
# nS1 <- nS + 1
# v_shifted1 <- roll(v, nS + 1)
#
# dT_flow <- v_shifted + pS * (v_shifted1 - v_shifted) - v
dT_flow <- advection.1D(v, v = vel, dx = 1, C.up = v[L], C.down = v[1],
adv.method = adv_method)$dC
dT <- dT_flow + dT_diff
# heating of the ring after the sensor
dT[sensorP + 1] <- dT[sensorP + 1] + y[L + 1]
# heat dispersion
dT <- dT - heatDisp * (v - baseTemp + 2.5 * sin(t/(60*24) * pi * 2))
return(list(c(dT, 0)))
}
out <- ode.1D(y = vec, times = 1:simTime, func = fun, parms = alpha, nspec = 1,
events = list(func = eventfun, root = T),
rootfunc = rootfun)
if (plot_type == 'sensors') {
## Trend of the temperature at the sensors levels
out %>%
{.[,c(1, sensorP + 1, sensorP + 3, L + 2)]} %>%
as.data.frame() %>%
setNames(c('time', 'pre', 'post', 'heat')) %>%
mutate(Amb = baseTemp + 2.5 * sin(time/(60*24) * pi * 2)) %>%
pivot_longer(-time, values_to = "val", names_to = "trend") %>%
ggplot(aes(time, val)) +
geom_hline(yintercept = thresh) +
geom_line(aes(color = trend)) +
theme_minimal() +
theme(panel.spacing=unit(0, "lines")) +
labs(x = 'time', y = 'T°', color = 'sensor')
} else {
## Trend of the temperature in the whole pipe
out %>%
as.data.frame() %>%
pivot_longer(-time, values_to = "val", names_to = "x") %>%
filter(time %in% round(seq.int(1, simTime, length.out = 40))) %>%
ggplot(aes(as.numeric(x), val)) +
geom_hline(yintercept = thresh) +
geom_line(alpha = .5, show.legend = FALSE) +
geom_point(aes(color = val)) +
scale_color_gradient(low = "#56B1F7", high = "red") +
facet_wrap(~ time) +
theme_minimal() +
theme(panel.spacing=unit(0, "lines")) +
labs(x = 'x', y = 'T°', color = 'T°')
}
}
Интересно, что установка большего количества сегментов (
L = 500) и высокая скорость (
vel = 2) можно наблюдать последовательность пиков в датчике дополнительного нагрева. Кроме того, время обработки резко увеличивается, но больше из-за увеличения скорости, чем из-за увеличения разрешения трубы.
Мое самое большое сомнение сейчас в том,
ReacTran::advection.1D() действительно имеет смысл в моем контексте, поскольку я моделирую температуру воды, в то время как эта функция, кажется, больше связана с концентрацией растворенного вещества в проточной воде.
1 ответ
Проблема выглядит как пример УЧП с подвижной и фиксированной фазой. Хорошее введение в подход «метода линий» (MOL) с R/deSolve можно найти в статье о ReachTran от Soetaert and Meysman (2012) doi.org/10.1016/j.envsoft.2011.08.011.
Пример PDE можно найти на слайде 55 некоторых слайдов семинара , больше в учебном пакете RTM.
R/deSolve/ReacTran пытается упростить ODE/PDE, но остаются подводные камни. Если возникает числовая дисперсия или осцилляции, это может быть вызвано нарушением условия Куранта-Фридрихса-Льюи .