Определить, является ли пересечение множества с соединением двух других множеств пустым

Question

Для любых трех заданных наборов A, B и C: есть ли способ определить (программно), существует ли элемент A, который является частью соединения (правка: пересечение) B и C?

пример:
A: все числа больше 3
B: все числа меньше 7
C: все числа, которые равны 5

В этом случае в наборе A есть элемент с номером 5, который подходит. Я реализую это как спецификации, так что этот числовой диапазон является лишь примером. A, B, C может быть чем угодно.

Answer 1

РЕДАКТИРОВАТЬ: Спасибо, Ники!

Будет полезно, если B.Count <= C.Count <= A.Count,

D = GetCommonElements(B,C);
if( D.Count>0 && GetCommonElements(D,A).Count >0)
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

SET GetCommonElements(X,Y)
{
    common = {}
    for x in X:
       if Y.Contains(x):
         common.Add(x);
    return common;
}

Посмотрите на эффективный алгоритм пересечения множеств.

---

Мы можем использовать законы распределения множеств

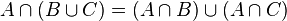
if(HasCommonElements(A,B) || HasCommonElements(A,C))
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

bool HasCommonElements(X,Y)
{
    // if at least one common element is found return true(immediately)

    return false
}

Answer 2

Если я правильно понимаю ваш вопрос, вы хотите программно вычислить пересечение 3 сетов, верно? Вы хотите увидеть, существует ли элемент в A, который существует на пересечении B и C, или, другими словами, вы хотите знать, является ли пересечение A, B и C непустым.

Во многих языках установлены контейнеры и алгоритмы пересечений, поэтому вы должны просто иметь возможность их использовать. Ваш пример в OCaml:

module Int = struct
    type t = int
    let compare i j = if i<j then -1 else if i=j then 0 else 1
end;;

module IntSet = Set.Make(Int);;

let a = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [4;5;6;7;8;9;10];;
let b = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [0;1;2;3;4;5;6];;
let c = IntSet.add 5 IntSet.empty;;

let aIbIc = IntSet.inter (IntSet.inter b c) a;;
IntSet.is_empty aIbIc;;

Это выводит false, поскольку пересечение ab и c непусто (содержит 5). Это, конечно, зависит от того, что элементы набора сравнимы (в примере функция сравнения определяет это свойство в модуле Int).

В качестве альтернативы в C++:

#include<iostream>
#include<set>
#include<algorithm>
#include<iterator>

int main()
{
    std::set<int> A, B, C;

    for(int i=10; i>3; --i)
        A.insert(i);
    for(int i=0; i<7; ++i)
        B.insert(i);
    C.insert(5);

    std::set<int> ABC, BC;
    std::set_intersection(B.begin(), B.end(), C.begin(), C.end(), std::inserter(BC, BC.begin()));
    std::set_intersection(BC.begin(), BC.end(), A.begin(), A.end(), std::inserter(ABC, ABC.begin()));

    for(std::set<int>::iterator i = ABC.begin(); i!=ABC.end(); ++i)
    {
        std::cout << *i << " ";
    }
    std::cout << std::endl;

    return 0;
}

Answer 3

Вопрос требует дальнейшего уточнения. Во-первых, вы хотите работать с символьными наборами, заданными диапазоном? И во-вторых, это вопрос разовый или будет повторяться в какой-то форме (если да, каковы устойчивые части вопроса?)?

Если вы хотите работать с диапазонами, вы можете представить их с помощью двоичных деревьев и определить операции объединения и пересечения для этих структур. Для построения дерева потребуется O(n log n), а для поиска результата потребуется O(log n). Это не окупится только с наборами деревьев, но будет гибким, чтобы эффективно поддерживать любую комбинацию диапазонов (если это то, что вы подумали, "это может быть что угодно").

С другой стороны, если что-то означает любой набор элементов, то единственный вариант - перечислить элементы. В этом случае построение деревьев B+ на множествах B и C также потребует O(n log n) времени, но здесь n - количество элементов, а в первом случае n - количество диапазонов. Последнее может быть на несколько порядков больше и, конечно, оно может представлять только конечное число элементов.