Как решить систему ОДУ с параметрами, зависящими от времени в R?

Question

Я пытаюсь решить эту систему ODE через deSolve, dX / dt = -X*a + (YX) b + c и dY / dt = -Ya + (XY)*b для времени [0,200], a= 0,30, b= 0,2, но c равно 1 для времени [50,70] и 0 в противном случае. Код, который я использовал,

      time <- seq(0, 200, by=1)
parameters <- c(a=0.33, b=0.2, c=1)
state <- c(X = 0, Y = 0)

    two_comp <- function(time, state, parameters){
      with(as.list(c(state, parameters)), {
        dX = -X*a + (Y-X)*b + c
        dY = -Y*a + (X-Y)*b
        return(list(c(dX, dY)))
      })
    }

out <- ode(y = state, times = time, func = two_comp, parms = parameters)
out.df = as.data.frame(out)

Я не учел изменяющуюся во времени часть параметра c, так как не могу найти способ включить ее и запустить ее плавно. Я попытался включить его в определения функций, но безуспешно. Пожалуйста помоги.

Answer 1

Стандартный способ - использовать approxfun, т.е. создать сигнал, зависящий от времени, который мы также называем переменной принуждения:

      library("deSolve")
time <- seq(0, 200, by=1)
parameters <- c(a=0.33, b=0.2, c=1)
state <- c(X = 0, Y = 0)

two_comp <- function(time, state, parameters, signal){
  cc <- signal(time)
  with(as.list(c(state, parameters)), {
    dX <- -X * a + (Y - X) * b + cc
    dY <- -Y * a + (X - Y) * b
    return(list(c(dX, dY), c = cc))
  })
}

signal <- approxfun(x = c(0, 50, 70, 200), 
                    y = c(0, 1,  0,  0), 
                    method = "constant", rule = 2)

out <- ode(y = state, times = time, func = two_comp, 
           parms = parameters, signal = signal)
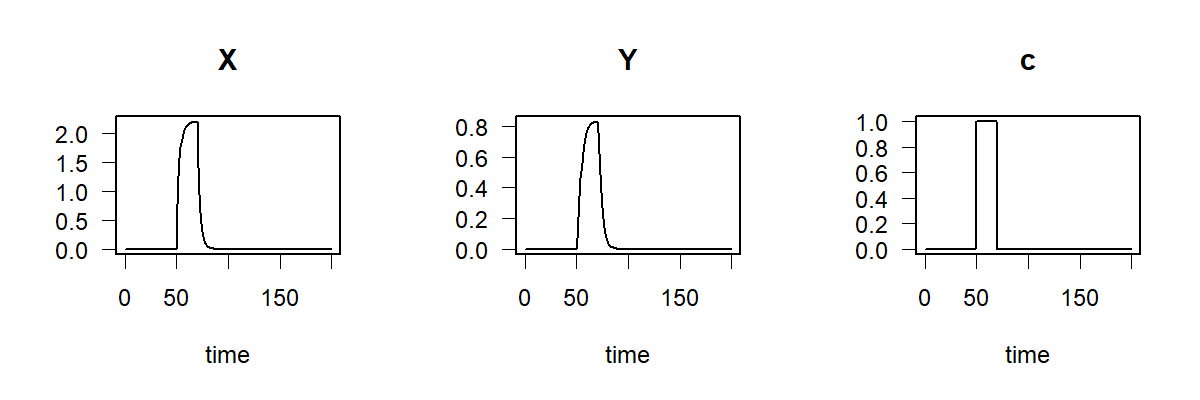
plot(out)

Также обратите внимание на специфичный для deSolve plot функция и что зависящая от времени переменная cc используется как дополнительная выходная переменная.

Подробнее об этом можно узнать:

• в ?forcings справочная страница и
• в кратком руководстве по Github.

Answer 2

Пределы интервала, где равно 1, можно передать как parameters. Затем внутри дифференциальной функции используйте их для создания логического значения.

      time >= lower & time <= upper

С FALSE/TRUE кодируются как целые числа 0/1, каждый раз, когда это условие ложно, c умножается на ноль, и дело в шляпе.

      library(deSolve)

two_comp <- function(time, state, parameters){
  with(as.list(c(state, parameters)), {
    dX = -X*a + (Y-X)*b + c*(time >= lower & time <= upper)
    dY = -Y*a + (X-Y)*b
    return(list(c(dX, dY)))
  })
}

time <- seq(0, 200, by=1)
parameters <- c(a=0.33, b=0.2, c=1, lower = 50, upper = 70)
state <- c(X = 0, Y = 0)

out <- ode(
  y = state, 
  times = time, 
  func = two_comp, 
  parms = parameters
)

out.df <- as.data.frame(out)
head(out.df)

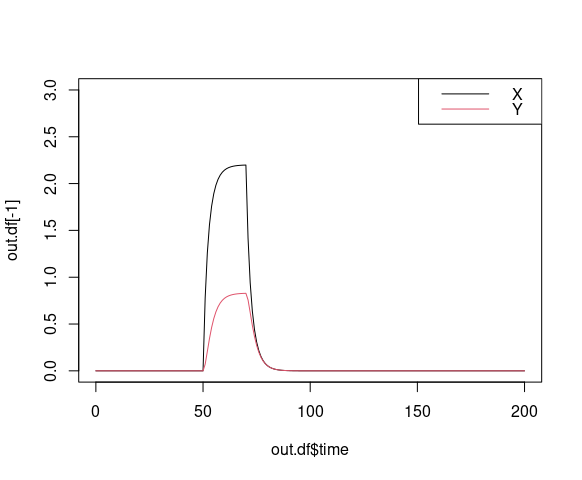
matplot(out.df$time, out.df[-1], type = "l", lty = "solid", ylim = c(0, 3))
legend("topright", legend = names(out.df)[-1], col = 1:2, lty = "solid")