Соединить четное количество узлов без пересечения

Question

У меня есть два набора из n узлов. Теперь я хочу соединить каждый узел из одного набора с другим узлом из другого набора. Полученный граф не должен иметь пересечений.

Я знаю несколько алгоритмов линии развертки (алгоритм Бентли-Оттмана, чтобы проверить, где происходят пересечения, но я не смог найти алгоритм для решения этих пересечений, за исключением подхода с использованием грубой силы).

Каждый узел из одного набора может быть подключен к любому другому узлу в другом наборе.

Любые указатели на (эффективный) алгоритм, который решает эту проблему? Нет необходимости в реализации.

EDIT1:

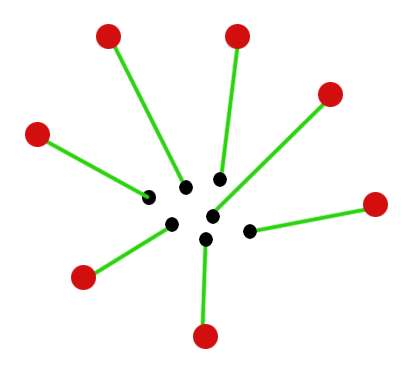
Вот одно решение проблемы для n=7:

Черные точки - это набор узлов, а красные точки - это набор. Каждый черный узел должен быть подключен к одному красному узлу, чтобы соединяющие их линии не пересекались.

EDIT2:

Для дальнейшего уточнения: позиции всех узлов фиксированы, и результирующий граф будет иметь n ребер. У меня также нет никаких доказательств того, что решение существует, но я не смог создать пример, где не было решения. Я уверен, что где-то есть доказательства того, что создание такого плоского графа всегда возможно. Кроме того, требуется только одно решение, а не все возможные решения.

Answer 1

Когда решение существует (см. Мой комментарий с примером, где его нет), его можно найти, найдя минимальный весовой коэффициент в полном двудольном графе, который содержит (красную или черную) вершину для каждой точки и для каждой красной вершина u и черная вершина v, ребро (u, v) веса, равное евклидову расстоянию между их соответствующими точками. Это можно оптимально решить за O(V^4) времени.

Почему это должно работать? Основная идея, которую я взял из ответа Дэвида Эйзенстата на аналогичный вопрос, состоит в том, что всякий раз, когда у нас есть пара отрезков AB и CD, которые пересекаются в некоторой точке X, неравенство треугольника можно использовать, чтобы показать, что выбор любой конечной точки каждого и замена их дает пару отрезков линии с меньшей или равной общей длиной:

A
|\
| \
|  \ X
C---+-----D
     \   /
      \ /
       B

AX + XC >= AC (tri. ineq.)
BX + XD >= BD (tri. ineq.)
AX + XC + BX + XD >= AC + BD (sum both sides)
(AX + BX) + (XC + XD) >= AC + BD (rearrange LHS)
   AB     +    CD     >= AC + BD (combine pairs of segments on LHS)

Предполагая далее, что треугольники AXC и BXC невырождены, >= становится >, (Достаточным условием для этого является то, что ни один набор из 3 точек, содержащих как минимум 1 красную и 1 черную точки, не является коллинеарным.) Таким образом, для любого данного решения (присвоение красных узлов черным узлам), если это решение содержит пересечение, то его общая сумма длин отрезков может быть уменьшена на ненулевое значение путем замены красных (или черных) конечных точек двух пересекающихся отрезков.

Другими словами,

Solution contains a crossing => sum of segment lengths is not minimal.

Взяв противозачаточное, мы сразу получаем

Sum of segment lengths is minimal => solution contains no crossing.

Поскольку алгоритм сопоставления минимального веса возвращает решение минимально возможного веса, это устанавливает его правильность.

(Обратите внимание, что нет необходимости беспокоиться о том, действительно ли перестановка конечных точек гарантирует, что новая пара отрезков AC и BD не пересекается - хотя кажется очевидным, что они не будут, все, что нам на самом деле нужно для доказательство правильности состоит в том, чтобы показать, что crossing exists => sum not minimal.)