Как нарисовать плоскость раздела из алгоритма классификации на трехмерном графике в R

Question

Я пытаюсь нарисовать границу раздела из алгоритма классификации на трехмерном графике в R (используя plot3D). Это относительно простая задача, если у нас есть только два предиктора, и для рисования требуется только две оси (например, с использованием функции). Я еще не нашел удовлетворительного способа нарисовать раздел классификации на основе трех предикторов в трехмерном пространстве.

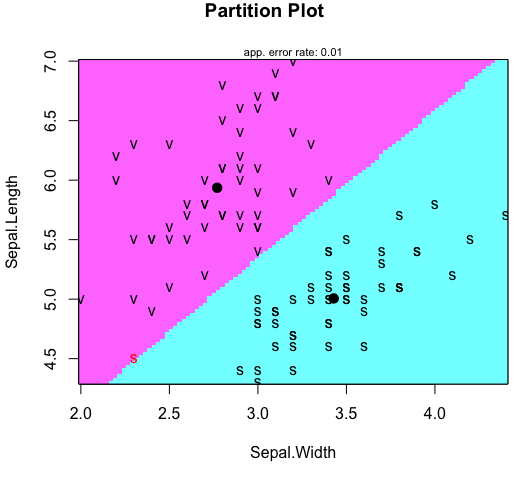
Чтобы визуализировать проблему, давайте начнем с создания раздела всего для двух осей, используя алгоритм классификации линейного дискриминантного анализа (LDA) для набора данных радужной оболочки глаза:

      # Load packages and subset the iris dataset:
library(klaR)

data = droplevels(iris[iris$Species != 'virginica', ])

partimat(Species ~ Sepal.Length + Sepal.Width, data, 
         method = 'lda')

Получается двухмерный график с четко обозначенным разделением между двумя видами:

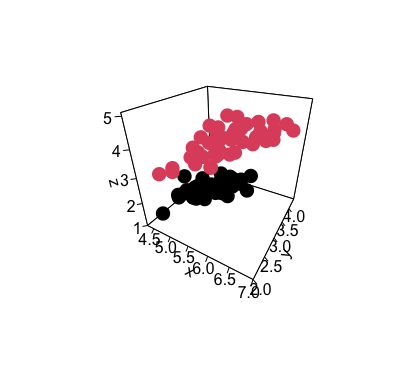
Тем не мение, partimat может обрабатывать только два предиктора одновременно (см. ?partimat). Давайте теперь посмотрим на 3D-проблему:

      library(plot3D)
    
# Plot the raw data:
points3D(data$Sepal.Length, data$Sepal.Width, data$Petal.Length,
             colkey = F,
             pch = 16, cex = 2,
             theta = 30, phi = 30, 
             ticktype = 'detailed',
             col = data$Species)

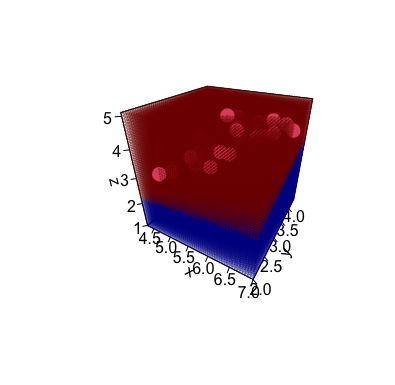
Я хочу нарисовать плоскость, разделяющую два класса данных, на основе алгоритма классификации, такого как LDA. Вдохновленный , вот моя примером Романа Луштриканеудачная попытка определить разделение между тремя предикторами. По сути, я построил модель LDA с тремя предикторами, а затем спрогнозировал вид (setosa или versicolor) на несколько точек между максимумами. и мин. значения всех трех предикторов. При нанесении на трехмерный график это создает облако точек, окрашенное по-разному, чтобы представить трехмерное пространство, в котором должен появиться любой вид радужной оболочки на основе трех предикторов:

      # Build a classification model with three predictors:
m = lda(Species ~ Sepal.Length + Sepal.Width + Petal.Length, data)

# Predict 'Species' for the full range of each plant metric: 
np = 50

nx = seq(from = min(data[, 1]), to = max(data[, 1]), length.out = np)
ny = seq(from = min(data[, 2]), to = max(data[, 2]), length.out = np)
nz = seq(from = min(data[, 3]), to = max(data[, 3]), length.out = np)
nd = expand.grid(Sepal.Length = nx, Sepal.Width = ny, Petal.Length = nz)

p    = as.numeric(predict(m, newdata = nd)$class)
part = cbind(nd, Partition = p)

# Plot the partition and add the data points:  
scatter3D(part$Sepal.Length, part$Sepal.Width, part$Petal.Length, 
          colvar = part$Partition, 
          colkey = F,
          alpha = 0.5,
          pch = 16, cex = 0.3, 
          theta = 30, phi = 30, 
          ticktype = 'detailed',
          plot = F)
points3D(data$Sepal.Length, data$Sepal.Width, data$Petal.Length,
         colkey = F,
         pch = 16, cex = 2,
         theta = 30, phi = 30, 
         ticktype = 'detailed',
         col = data$Species,
         add = T)

Я также добавил точки данных. Вы можете различить разделение как нечеткое пересечение синего и красного в облаке точек:

Это не идеальное решение, так как трудно увидеть точки данных, скрытые в облаке точек. Облако точек тоже немного отвлекает. Может быть, какое-то умное построение точек с прозрачностью улучшит ситуацию, но я подозреваю, что гораздо более приятным решением было бы нарисовать плоскость (похожую на плоскость регрессии ) на пересечении между классами видов (то есть там, где встречаются синие и красные точки). Обратите внимание, что в конечном итоге я хочу использовать разные классификаторы (например, случайный лес) на случай, если есть решение, ограниченное только LDA или аналогичным.

Большое спасибо за любые решения или советы.

Answer 1

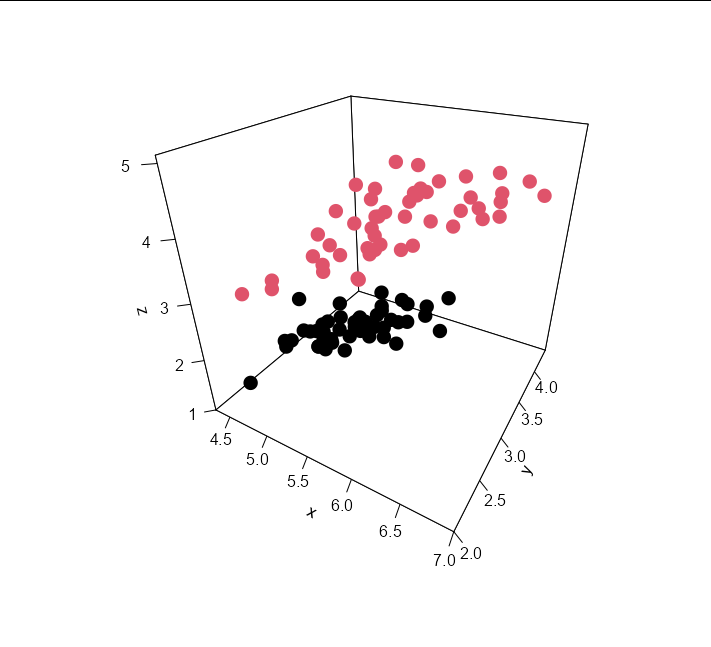
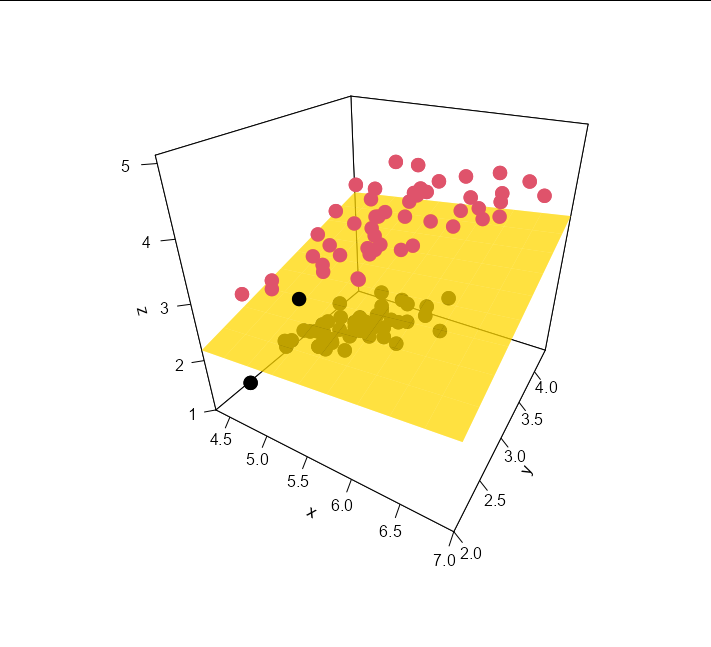
Вы можете использовать коэффициенты из модели lda, чтобы сгенерировать плоскость, разделяющую дискриминантные объемы. По сути, плоскость представляет собой набор точек в трехмерном пространстве, где сумма координат (x, y, z), умноженных на их соответствующие коэффициенты из модели, равна порогу модели (т. е. плоскости, на которой модель может не отличать одну группу от другой).

Мы можем сделать это, создав сетку 10 x 10 равноотстоящих значений вдоль осей x и y и вычислив значение z, которое дает нам пороговое значение на основе модели:

      threshold <-  sum(coef(m) * data[1, 1:3]) - predict(m)$x[1] 

Sepal_Lengths <- seq(min(data$Sepal.Length), max(data$Sepal.Length), length.out = 10)
Sepal_Widths  <- seq(min(data$Sepal.Width), max(data$Sepal.Width), length.out = 10)
Petal_Lengths <- outer(Sepal_Lengths, Sepal_Widths, function(x, y) {
                  (threshold - x * coef(m)[1] - y * coef(m)[2]) / coef(m)[3]})

Итак, теперь, когда мы рисуем наши точки:

      points3D(data$Sepal.Length, data$Sepal.Width, data$Petal.Length,
         colkey = F,
         pch = 16, cex = 2,
         theta = 30, phi = 30, 
         ticktype = 'detailed',
         col = data$Species)

Добавить самолет так же просто, как:

      persp3D(x = Sepal_Lengths, 
        y = Sepal_Widths, 
        z = Petal_Lengths, 
        col = "gold", add = TRUE, alpha = 0.5)