Определение значений X для кода

Question

У меня есть эта задача, чтобы создать скрипт, который работает аналогично normcdf на Matlab.

       x=linspace(-5,5,1000); %values for x
       p= 1/sqrt(2*pi) * exp((-x.^2)/2); % THE PDF for the standard normal 
       t=cumtrapz(x,p); % the CDF for the standard normal distribution
       plot(x,t); %shows the graph of the CDF

Проблема в том, когда t значения присваиваются 1: 1000 вместо -5:5 с шагом. Я хочу знать, как назначить правильные значения х, то есть -5:5,1000 для вывода значений t? например, когда я делаю t(n) Я получаю тот же результат, что и normcdf(n),

Просто чтобы уточнить: проблема в том, что я не могу просто сказать, t(-5) и получить результат =1, как я бы в normcdf(1) потому что вычисленные значения cumtrapz присваиваются x=1:1000 вместо от -5 до 5.

Answer 1

Обновленный ответ

Хорошо, прочитав ваш комментарий; Вот как делать то, что вы хотите:

x = linspace(-5,5,1000);
p = 1/sqrt(2*pi) * exp((-x.^2)/2);
cdf = cumtrapz(x,p);

q = 3; % Query point
disp(normcdf(q)) % For reference
[~,I] = min(abs(x-q)); % Find closest index
disp(cdf(I)) % Show the value

К сожалению, нет синтаксиса Matlab, который будет делать это красиво в одной строке, но если вы абстрагируете поиск ближайшего индекса в другую функцию, вы можете сделать это:

cdf(findClosest(x,q))

function I = findClosest(x,q)
if q>max(x) || q<min(x)
    warning('q outside the range of x');
end
[~,I] = min(abs(x-q));
end

Также; если вы уверены, что точное значение точки запроса q существует в x можно просто сделать

cdf(x==q);

Но остерегайтесь ошибок с плавающей запятой. Вы можете подумать, что определенный диапазон должен содержать определенное значение, но мало ли вы знали, что он отличается от крошечного округления erorr. Вы можете увидеть это в действии, например, здесь:

x1 = linspace(0,1,1000); % Range
x2 = asin(sin(x1)); % Ought to be the same thing
plot((x1-x2)/eps); grid on; % But they differ by rougly 1 unit of machine precision

Старый ответ

Насколько я могу судить, выполнение вашего кода воспроизводит результат normcdf(x) хорошо... Если вы хотите сделать именно то , что normcdf использует их erfc,

close all; clear; clc;

x = linspace(-5,5,1000);
cdf = normcdf(x); % Result of normcdf for comparison

%% 1 Trapezoidal integration of normal pd
p = 1/sqrt(2*pi) * exp((-x.^2)/2);
cdf1 = cumtrapz(x,p);

%% 2 But error function IS the integral of the normal pd
cdf2 = (1+erf(x/sqrt(2)))/2;

%% 3 Or, even better, use the error function complement (works better for large negative x)
cdf3 = erfc(-x/sqrt(2))/2;

fprintf('1: Mean error = %.2d\n',mean(abs(cdf1-cdf)));
fprintf('2: Mean error = %.2d\n',mean(abs(cdf2-cdf)));
fprintf('3: Mean error = %.2d\n',mean(abs(cdf3-cdf)));
plot(x,cdf1,x,cdf2,x,cdf3,x,cdf,'k--');

Это дает мне

1: Mean error = 7.83e-07
2: Mean error = 1.41e-17
3: Mean error = 00 <- Because that is literally what normcdf is doing

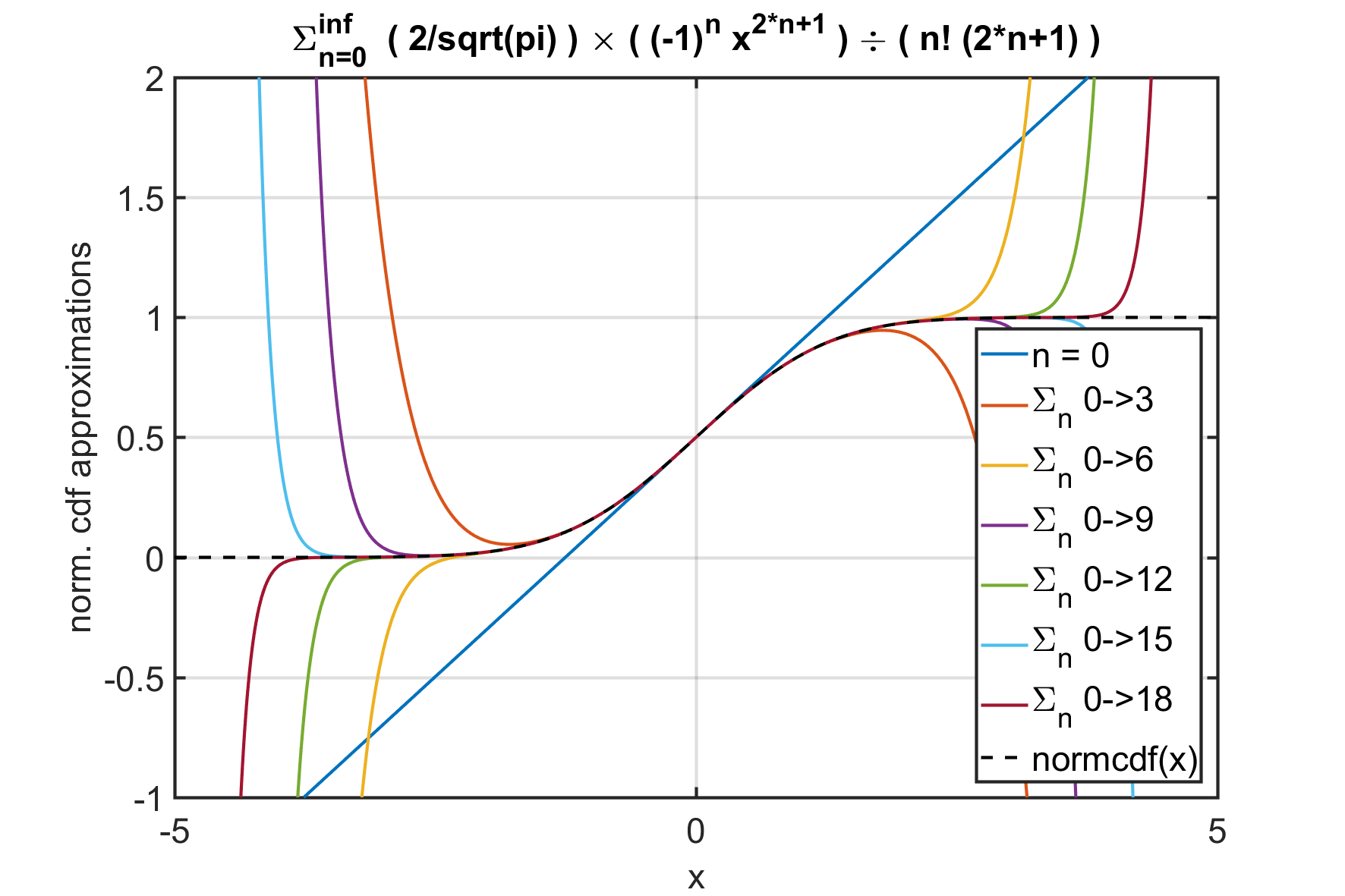
Если ваша цель не в том, чтобы использовать предопределенные функции matlab, а вместо того, чтобы вычислить результат численно (то есть вычислить функцию ошибки), то это интересный вызов, о котором вы можете прочитать, например, здесь или в этом посте об обмене статистикой стека. В качестве примера, следующий фрагмент кода вычисляет функцию ошибки путем реализации eq. 2 Форма первой ссылки:

nerf = @(x,n) (-1)^n*2/sqrt(pi)*x.^(2*n+1)./factorial(n)/(2*n+1);

figure(1); hold on;
temp = zeros(size(x)); p =[];
for n = 0:20
    temp = temp + nerf(x/sqrt(2),n);
    if~mod(n,3)
        p(end+1) = plot(x,(1+temp)/2);
    end
end
ylim([-1,2]);
title('\Sigma_{n=0}^{inf}  ( 2/sqrt(pi) ) \times ( (-1)^n x^{2*n+1} ) \div ( n! (2*n+1) )');
p(end+1) = plot(x,cdf,'k--');
legend(p,'n = 0','\Sigma_{n} 0->3','\Sigma_{n} 0->6','\Sigma_{n} 0->9',...
    '\Sigma_{n} 0->12','\Sigma_{n} 0->15','\Sigma_{n} 0->18','normcdf(x)',...
    'location','southeast');
grid on; box on;
xlabel('x'); ylabel('norm. cdf approximations');

Answer 2

Ответ Марцина предлагает способ найти ближайшую точку выборки. ИМО проще интерполировать. Дано x а также t как определено в вопросе,

interp1(x,t,n)

возвращает оценочную стоимость CDF в x==nдля любой стоимости n, Но обратите внимание, что для значений за пределами вычисленного диапазона он будет экстраполироваться и давать ненадежные значения.

Вы можете определить анонимную функцию, которая работает как normcdf:

my_normcdf = @(n)interp1(x,t,n);

my_normcdf(-5)

Answer 3

Попробуйте заменить х на 0,01 при вызове cumtrapz. Вы можете использовать вектор или скалярный интервал для cumtrapz ( https://www.mathworks.com/help/matlab/ref/cumtrapz.html), и это может решить вашу проблему. Кроме того, вы проверили оригинальные значения х? Проблема в linspace (т.е. вы не получаете правильный вектор x) или в cumtrapz?