Как ограничена видимая гамма?

Question

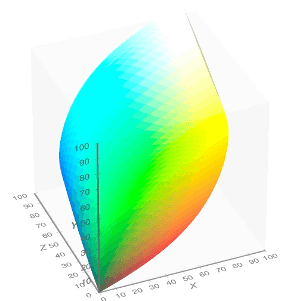
То, что координаты цвета в пространстве CIE XYZ представляют стимуляцию одного из типов конусов в наших глазах - отсюда и значения тристимул. Не все координаты (x, y, z) имеет смысл (например, у вас не может быть отрицательной стимуляции ни в одном из колбочек), поэтому доменом всех возможных комбинаций в пространстве XYZ будет капля. Иногда вы можете найти этот блоб, изображенный, например, в Википедии:

(Цвета на BLOB-объектах довольно бессмысленны, поскольку на самом деле их невозможно отобразить на стандартном мониторе RGB.)

Теперь я спрашиваю себя, почему этот блоб ограничен. Я не могу просто выбрать любую точку (x, y, z) в капле и масштабировать его с alpha*(x,y,z,)Как я бы включил источник света и все еще находился в видимом пространстве? Что именно составляет верхнюю границу здесь?

Answer 1

Определения контекста

Внешняя поверхность, изображенная на вашем изображении из Википедии, представляет объем, ограниченный функциями согласования цветов (CMFS). CMFS определяются CIE следующим образом:

трехцветные значения монохроматических стимулов равной мощности излучения

Другое название источника света с равной мощностью излучения в системе CIE - Equal Energy или E.

Значения CIE XYZ tristimulus сами определяются CIE:

количество 3 эталонных цветовых стимулов в данной трихроматической системе, необходимое для соответствия цвету рассматриваемого стимула

Это напрямую связано с экспериментами по подбору цветов Максвелла и Райта и Гильдии (1931) и, вероятно, выходит за рамки этого ответа.

Генерация внешней поверхности

Внешняя поверхность, вероятно, построена с использованием прямоугольных спектральных распределений мощности (SPD), то есть срезов источника света с равной энергией. У Брюса Линдблума есть объяснение на этой странице.

Методология состоит в том, чтобы преобразовать прямоугольные SPD с различной шириной полосы в значения CIE XYZ tristimulus, это сформирует внешнюю поверхность.

Предполагая 5 корзин, первый набор SPD будет таким:

1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

Второй:

1 1 0 0 0
0 1 1 0 0
0 0 1 1 0
0 0 0 1 1
1 0 0 0 1

Третий:

1 1 1 0 0
0 1 1 1 0
0 0 1 1 1
1 0 0 1 1
1 1 0 0 1

так далее...

Вот фрагмент кода Python, использующий Color для генерации точек для внешней поверхности:

import colour
import numpy as np


class NearestNeighbourInterpolator(colour.KernelInterpolator):
    def __init__(self, *args, **kwargs):
        kwargs['kernel'] = colour.kernel_nearest_neighbour
        super(NearestNeighbourInterpolator, self).__init__(*args, **kwargs)


def generate_square_waves(samples):
    square_waves = []
    square_waves_basis = np.tril(np.ones((samples, samples)))[0:-1, :]
    for i in range(samples):
        square_waves.append(np.roll(square_waves_basis, i))
    return np.vstack((np.zeros(samples), np.vstack(square_waves),
                    np.ones(samples)))


def XYZ_outer_surface(samples):
    XYZ = []
    wavelengths = np.linspace(colour.DEFAULT_SPECTRAL_SHAPE.start,
                            colour.DEFAULT_SPECTRAL_SHAPE.end, samples)

    for wave in generate_square_waves(samples):
        spd = colour.SpectralPowerDistribution(
            wave, wavelengths).align(
                colour.DEFAULT_SPECTRAL_SHAPE,  
                interpolator=NearestNeighbourInterpolator)
        XYZ.append(colour.spectral_to_XYZ(spd))

    return np.array(XYZ).reshape(len(XYZ), -1, 3)


# 43 is picked as number of samples to have integer wavelengths.
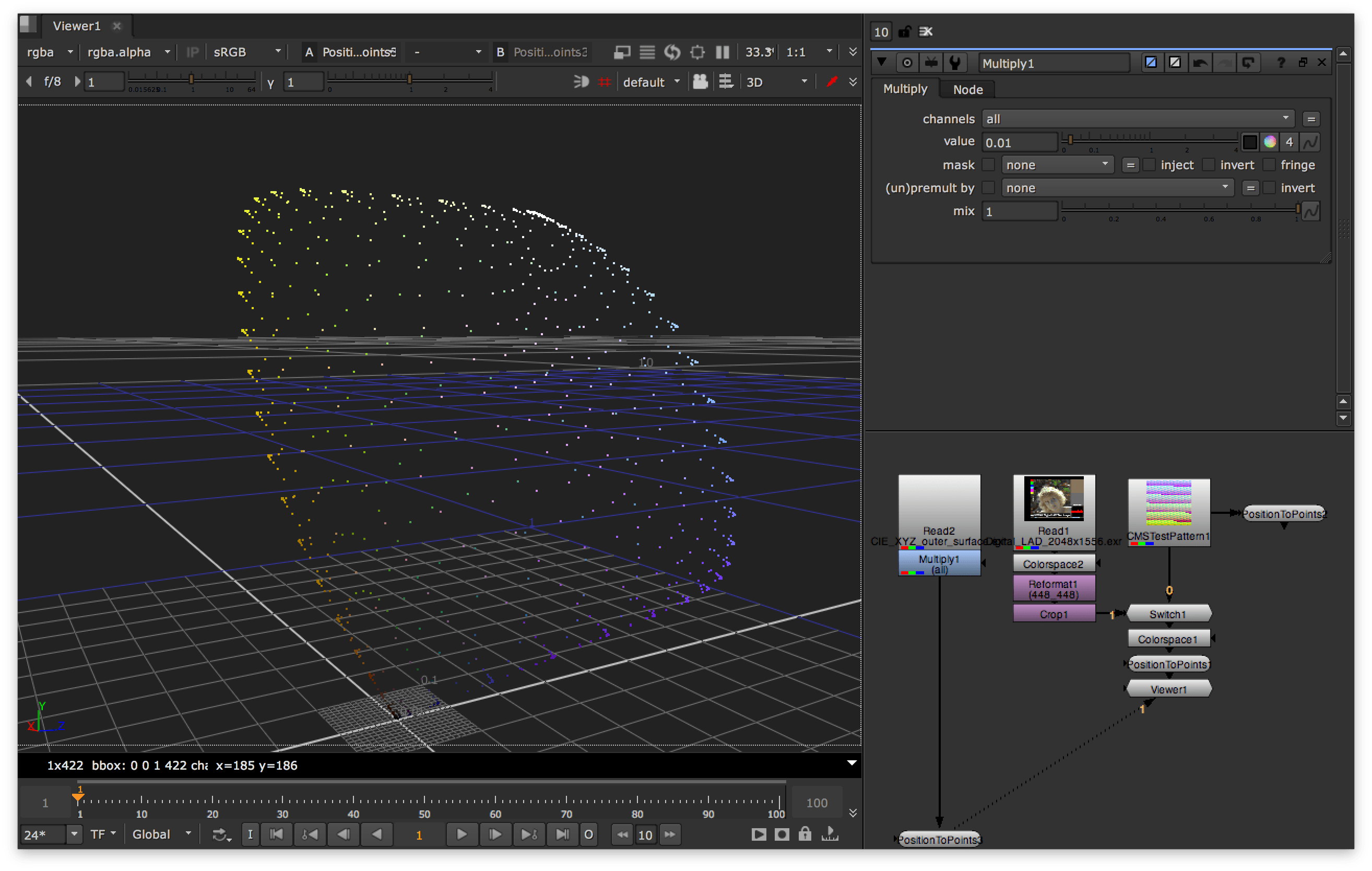
colour.write_image(XYZ_outer_surface(43), 'CIE_XYZ_outer_surface.exr')

И вывод: