lsoda создает вымышленные ценности?

Question

В настоящее время я разрабатываю модель для интеграции микробиологии и геохимии, в которой lsoda используется для решения большого количества дифференциальных уравнений. Модель слишком велика, чтобы размещать ее здесь, потому что она состоит из нескольких модулей, но у меня происходит очень странное событие.

Это мои начальные значения, введите описание изображения здесь

Я инициализировал их как нулевые, потому что я не хочу никаких микробов, просто чтобы проверить, как изменится химический состав без микробов. Однако после 5 или 6 шагов я начинаю видеть значения, отличные от нуля в некоторых из моих микробных переменных:введите здесь описание изображения .

Интересно, может быть, lsoda выполняет какой-то раунд, и поэтому я получаю эти значения, потому что в противном случае я не могу объяснить, откуда эти значения появляются. Если это так, кто-нибудь знает, как остановить подобные облавы?

Answer 1

Короткий ответ

Нет, не создает «вымышленных» значений.

Подробный ответ

Как заявил @Ben Bolker, «арифметика с плавающей запятой по своей сути неточна». Я хочу добавить, что все решатели, включая вычисление приближений, и что нелинейные модели могут увеличивать ошибки.

Вы можете проверить свою модель, если все производные равны нулю, вызвав функцию модели отдельно, без решателя, см. следующий пример системы Лоренца, где все состояния установлены равными нулю:

      library(deSolve)

Lorenz <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
    dX <-  a * X + Y * Z
    dY <-  b * (Y - Z)
    dZ <- -X * Y + c * Y - Z
    list(c(dX, dY, dZ))
  })
}

parameters <- c(a = -8/3, b = -10, c = 28)
state      <- c(X = 0, Y = 0, Z = 0)
times      <- seq(0, 500, by = 1)

range(Lorenz(0, state, parameters))

что дает

      [1] 0 0

Контрпример

Если мы изменим модель так, чтобы одна производная немного отличалась от нуля из-за ошибки округления, например, используя пример Бена:

      Fancy  <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
    dX <-  a * X + Y * Z + 27 * (sqrt(X + Y + Z + 2)^2 - 2)
    dY <-  b * (Y - Z)
    dZ <- -X * Y + c * Y - Z
    list(c(dX, dY, dZ))
  })
}
range(Fancy(0, state, parameters))

тогда это дает:

      [1] 0.000000e+00 1.199041e-14

В зависимости от допусков такая модель может затем колебаться или даже взрываться. Удивительно, но меньшая переносимость иногда может быть хуже:

      out1 <- ode(y = state, times = times, func = Lorenz, parms = parameters, atol=1e-6)
out2 <- ode(y = state, times = times, func = Fancy, parms = parameters, atol=1e-6)
out3 <- ode(y = state, times = times, func = Fancy, parms = parameters, atol=1e-8)

par(mfrow=c(3,1))
plot(out1[,1:2], type="l", main="Lorenz, derivatives = 0")
plot(out2[,1:2], type="l", main="Fancy, small error in derivatives, atol=1e-6")
plot(out3[,1:2], type="l", main="Fancy, small error in derivatives, atol=1e-8")

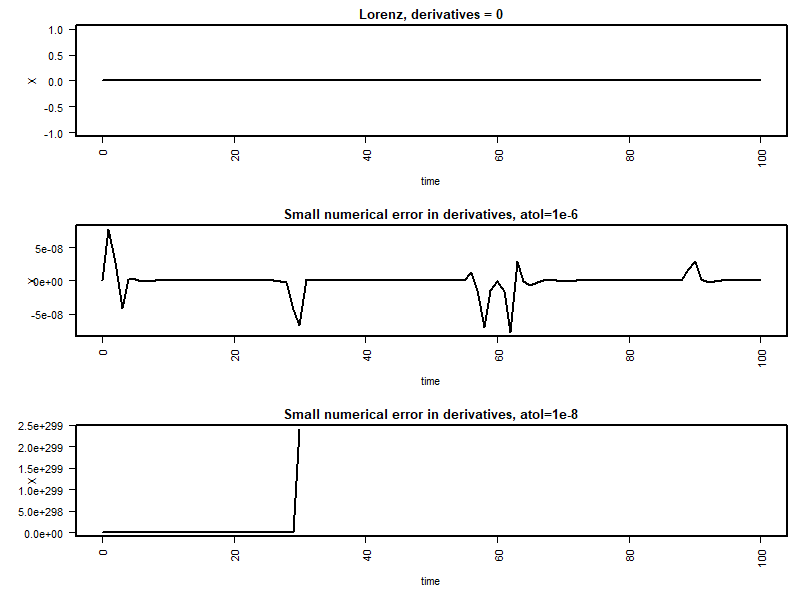
Вывод

• lsodaхорошо работает в рамках ограничений арифметики с плавающей запятой.
• модели должны быть тщательно разработаны и протестированы.