Эквивалент Python/Numpy изоповерхностных функций MATLAB
Любой может предложить эквивалентную функцию функции MATLABisosurface в python / numpy. Изоповерхность MATLAB возвращает грани и вершины. Мне нужны грани и вершины для создания файлов .stl. Функция MATLABisosurface выглядит так:
[f,v] = isosurface(X,Y,Z,V,isovalue)
в python я нашел этот метод, который работает следующим образом:
import plotly.graph_objects as go
import numpy as np
X, Y, Z = np.mgrid[-5:5:40j, -5:5:40j, -5:5:40j]
# ellipsoid
values = X * X * 0.5 + Y * Y + Z * Z * 2
fig = go.Figure(data=go.Isosurface(
x=X.flatten(),
y=Y.flatten(),
z=Z.flatten(),
value=values.flatten(),
isomin=10,
isomax=40,
caps=dict(x_show=False, y_show=False)
))
fig.show()
проблема с этим методом заключается в том, что он строит только изоповерхности и не возвращает грани и вершины, как это делает функция MATLABisosurface, и мне нужны эти грани и вершины.
Любая помощь будет принята с благодарностью.
3 ответа
созданная на основе VTK, не входит в число ваших целевых библиотек, PyVista,но может помочь вам в этом легко. Поскольку в комментариях вы казались восприимчивыми к решению на основе PyVista, вот как вы это сделаете:
- определить сетку, как правило, как
StructuredGridдля вашего типа данных, хотя эквидистантная сетка в вашем примере может даже работать сUniformGrid, - вычислить его изоповерхности с помощью
contourфильтр, - сохранить как файл, используя
saveметод сетки, содержащей изоповерхности.
import numpy as np
import pyvista as pv
# generate data grid for computing the values
X, Y, Z = np.mgrid[-5:5:40j, -5:5:40j, -5:5:40j]
values = X**2 * 0.5 + Y**2 + Z**2 * 2
# create a structured grid
# (for this simple example we could've used an unstructured grid too)
# note the fortran-order call to ravel()!
mesh = pv.StructuredGrid(X, Y, Z)
mesh.point_arrays['values'] = values.ravel(order='F') # also the active scalars
# compute 3 isosurfaces
isos = mesh.contour(isosurfaces=3, rng=[10, 40])
# or: mesh.contour(isosurfaces=np.linspace(10, 40, 3)) etc.
# plot them interactively if you want to
isos.plot(opacity=0.7)
# save to stl
isos.save('isosurfaces.stl')
Интерактивный сюжет выглядит примерно так: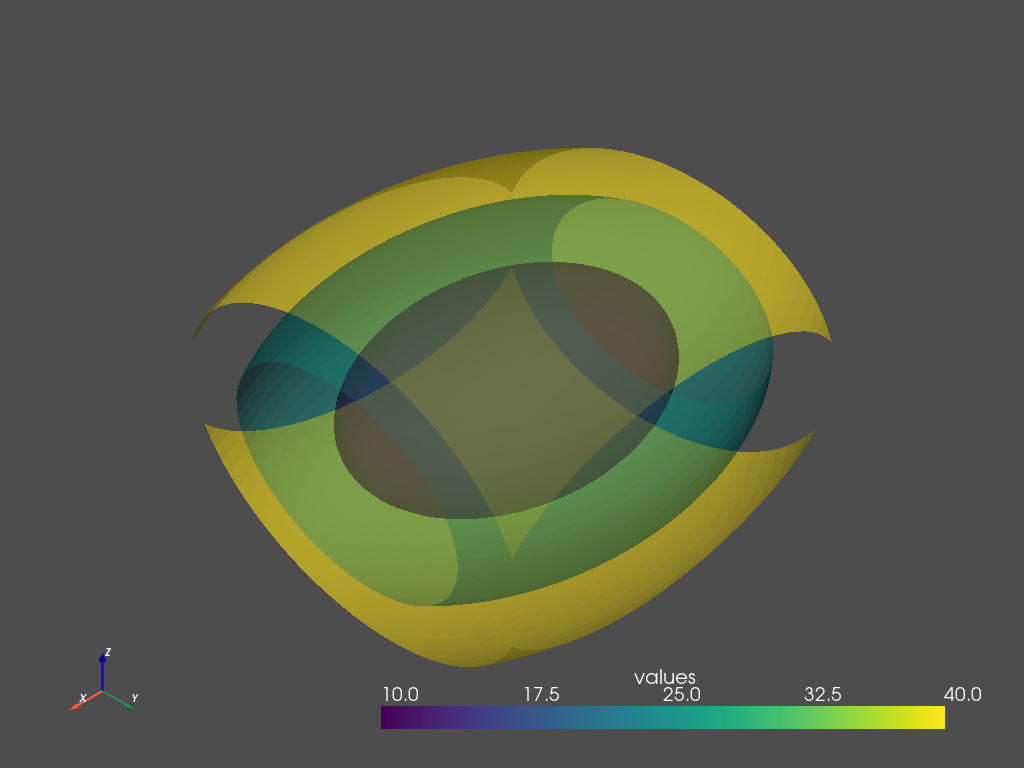
Цвета соответствуют значениям, выбранным из массива скаляров и обозначенным скалярной полосой.
Если мы загрузим сетку из файла, мы получим структуру, но не скаляры:
loaded = pv.read('isosurfaces.stl')
loaded.plot(opacity=0.7)
Причина отсутствия скаляров заключается в том, что массивы данных не могут быть экспортированы в
.stl файлы:
>>> isos # original isosurface mesh
PolyData (0x7fa7245a2220)
N Cells: 26664
N Points: 13656
X Bounds: -4.470e+00, 4.470e+00
Y Bounds: -5.000e+00, 5.000e+00
Z Bounds: -5.000e+00, 5.000e+00
N Arrays: 3
>>> isos.point_arrays
pyvista DataSetAttributes
Association: POINT
Contains keys:
values
Normals
>>> isos.cell_arrays
pyvista DataSetAttributes
Association: CELL
Contains keys:
Normals
>>> loaded # read back from .stl file
PolyData (0x7fa7118e7d00)
N Cells: 26664
N Points: 13656
X Bounds: -4.470e+00, 4.470e+00
Y Bounds: -5.000e+00, 5.000e+00
Z Bounds: -5.000e+00, 5.000e+00
N Arrays: 0
В то время как исходные изоповерхности имели привязанные к каждой изоповерхности (обеспечивающие цветовое отображение, показанное на первом рисунке), а также нормали точек и ячеек (вычисленные вызовом функции
.save() почему-то), в последнем случае данных нет.
Тем не менее, поскольку вы ищете вершины и грани, это должно подойти. Если вам это нужно, вы также можете получить к ним доступ на стороне PyVista, поскольку сетка isosurface является
PolyData объект:
>>> isos.n_points, isos.n_cells
(13656, 26664)
>>> isos.points.shape # each row is a point
(13656, 3)
>>> isos.faces
array([ 3, 0, 45, ..., 13529, 13531, 13530])
>>> isos.faces.shape
(106656,)
Теперь с логистикой лиц немного сложнее. Все они закодированы в 1d массиве целых чисел. В массиве 1d у вас всегда есть целое число, указывающее размер данного лица, а затем
nотсчитываемые от нуля индексы, соответствующие точкам в массиве точек. Вышеупомянутые изоповерхности полностью состоят из треугольников:
>>> isos.faces[::4] # [3 i1 i2 i3] quadruples encode faces
array([3, 3, 3, ..., 3, 3, 3])
Вот почему вы увидите
>>> isos.faces.size == 4 * isos.n_cells
True
и ты мог бы сделать
isos.faces.reshape(-1, 4) чтобы получить 2d-массив, где каждая строка соответствует треугольной грани (а первый столбец - константа 3).
В python/numpy нет эквивалентной функции «изоповерхности» MATLAB. Вам нужен Marching Cube из Scikit-image для возврата граней и вершин.
Метод Marching_cubes из scikit-image предоставляет вершины треугольников на изо-поверхности. Однако вершины находятся в терминах индексов 3D-функции. Чтобы преобразовать индексы в фактические координаты, мы можем использовать метод interp для 1D-интерполяции с помощью Numpy . Вот пример:
import numpy as np
import matplotlib.pyplot as plt
from skimage.measure import marching_cubes
...
x_coordinates = np.linspace(0, 1, 10)
y_coordinates = np.linspace(0, 1, 20)
z_coordinates = np.linspace(0, 1, 30)
...
def getLocationOnAxis(vertices:np.ndarray, axis:np.ndarray) -> np.ndarray :
return np.interp(vertices, np.arange(axis.shape[0]), axis)
# Note func_3D_values must be a 3D array
# with cartesian indexing, i.e.,
# func_3D_values.shape = (10, 20, 30)
vertices, faces, normals, values = marching_cubes(func_3D_values, level)
vertices_x = getLocationOnAxis(vertices[:, 0], x_coordinates)
vertices_y = getLocationOnAxis(vertices[:, 1], y_coordinates)
vertices_z = getLocationOnAxis(vertices[:, 2], z_coordinates)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_trisurf(vertices_x, vertices_y, vertices_z, triangles=faces)
Этот пример можно изменить для работы с любой прямолинейной трехмерной сеткой.
