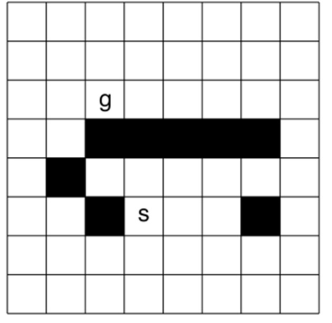
как лучший первый поиск определяет равные расстояния между узлами?

Question

Я работаю над этим назначением, но не понимаю, какой узел будет лучшим первым ходом поиска в следующий раз. используя расстояние Манхэттена, я обнаружил, что все узлы, которые напрямую связаны с начальным узлом, имеют одинаковое расстояние. Мой вопрос в том, что, поскольку это BFS, и я должен использовать расстояние Манхэттена в качестве функции оценки. как BFS решит, какой узел исследовать дальше.

Answer 1

спасибо за ответ, но что, если эвристическая стоимость двух соседних узлов по отношению к текущим узлам одинакова. Я имею в виду, что, поскольку этот алгоритм стремится к наименьшей стоимости и, предполагая, что у нас есть два равных наименьших значения, как алгоритм решает (на основе каких критериев)

Answer 2

      const getHeuristic = (row, col) => {
    return Math.abs(end.row - row) + Math.abs(end.col - col);
};

const NEIGHBORS = [
    [-1, 0],
    [0, 1],
    [1, 0],
    [0, -1],
];

const visitNeighbors = (node) => {
    let { row, col } = node;
    NEIGHBORS.forEach((neighbor) => {
        let r = row + neighbor[0];
        let c = col + neighbor[1];
        if (checkIndexes(matrix, r, c)) {
            //check to see if the neighbors of this node don't cause out of bounds issues. Like edge nodes.
            let cost = getHeuristic(r, c);
            pQueue.insert({ row: r, col: c, cost });
        }
    });
};

let begin = {
        row: start.row,
        col: start.col,
        cost: 0,
    };

pQueue.insert(begin);

while (pQueue.size() > 0) {
    let cell = pQueue.pop();
    if (isEquals(cell, end)) {
        //handle when end is found. If you want to trace the path, the use a map to keep track of the parent node when you explore its children.
return;
    }
    visitNeighbors(cell);
}

Для поиска Best-first,

1. Вы должны использовать эвристическую функцию, которая наилучшим образом оценивает расстояние до цели от текущего узла. Для расстояния Манхэттена эта функция может быть: Math.abs(goal.row - current.row) + Math.abs(goal.col - current.col). Здесь вы берете разницу между значениями строк и значений столбцов узла, который вы обрабатываете в данный момент, и целевого узла, и складываете их абсолютные значения вместе.

2. Тогда у вас будет очередь с приоритетом, в которую вы добавите соседей вместе с эвристической стоимостью, чтобы добраться до них.

3. Вы должны удалить узел с наименьшей стоимостью из очереди приоритетов на основе эвристического значения, исследовать каждого из его соседей и вычислить эвристическую стоимость, чтобы добраться до этих узлов и продвинуть их в очередь с приоритетами, и так далее, пока не достигнете конечного узла.

Если предполагаемые расстояния между узлами равны, то любой выбранный вами узел даст правильный результат. Best First Search не гарантирует кратчайшего пути. Но чтобы ответить на ваш вопрос, вам не нужно иметь тай-брейк, если они имеют одинаковую стоимость, просто удалите их из очереди приоритетов, все, что удаляется, все равно правильно. Если вам нужен кратчайший путь, изучите алгоритм A-Star.

PS для дальнейших разъяснений спрашивайте в комментариях, не стоит создавать ответ, чтобы задать другой вопрос / уточнение.