Как вычислить S-пары в Macaulay2?

Question

Алгоритм Бухбергера требует вычисления S-пар (подробнее на странице 83 "Идеалов, вариаций и алгоритмов" от Cox et al. 2008, 3-е издание)

S (f, g) = LCM (LT (f), LT (г))/LT(f) *f - LCM(LT(f),LT(г)) / LT (г) * г

где LCM - это наименьшее общее кратное (эквивалентно x^\gamma в нотации книги), а LT - ведущий член.

Как вы можете вычислить S-пары в Macaulay2 или другим способом программно?

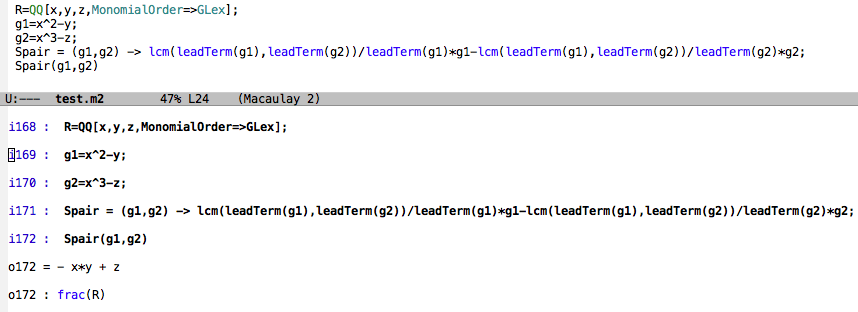
Пример: S-пара в градуированном лексикографическом порядке с g1=x^2-y и g2=x^3-z, где S(g1,g2)=xz-xy.

Answer 1

Команда S-pair для Macaulay2 как функция по определению

а также код в тексте для легкого копирования

Spair = (g1,g2) -> lcm(leadTerm(g1),leadTerm(g2))/leadTerm(g1)*g1-lcm(leadTerm(g1),leadTerm(g2))/leadTerm(g2)*g2;

это работает так, что Spair(polynomial1, polynomial2) вычисляет полином S-пары для полинома1 и полинома2.

Напротив, альтернативный метод для Спаррса, по-видимому, может быть выведен в терминах сизигий и образующих по теореме 9 книги (1).

S * G = \sum_{i=1}^t h_i g_i \rightarrow_G 0

где отображение по модулю G, S-пары так или иначе связаны с выражением в терминах сизигий и генераторов, некоторые примеры приведены ниже. Возможно, syz и gb полезны для вычисления S-пар.

Связь S-пар с образующими множествами в терминах базиса Грёбнера и сизигий

• "Давайте теперь посмотрим на первые сизигии (или минимальные S-пары [1, §2.9]) среди шестнадцати минимальных образующих." ( Идеалы, Многообразия и Маколей 2, p9)

• "The matrix spairs contains all the S-pairs between generators of J corresponding to the minimal first syzygies of M" (p.195 here)

Рекомендации

(1) Ideals, Varities, and Algorithms by Cox et all (2008, 3rd ed)