Как проверить понижающую дискретизацию, как задумано

Question

Как проверить правильность вывода с понижением частоты. Например, я сделал несколько примеров, однако я не уверен, что вывод правильный или нет?

Любая идея по валидации

Код

import numpy as np
import matplotlib.pyplot as plt # For ploting
from scipy import signal
import mne

fs = 100 # sample rate
rsample=50 # downsample frequency
fTwo=400 # frequency of the signal
x = np.arange(fs)
y = [ np.sin(2*np.pi*fTwo * (i/fs)) for i in x]
f_res = signal.resample(y, rsample)
xnew = np.linspace(0, 100, f_res.size, endpoint=False)
#
# ##############################
#
plt.figure(1)
plt.subplot(211)
plt.stem(x, y)
plt.subplot(212)
plt.stem(xnew, f_res, 'r')
plt.show()

Answer 1

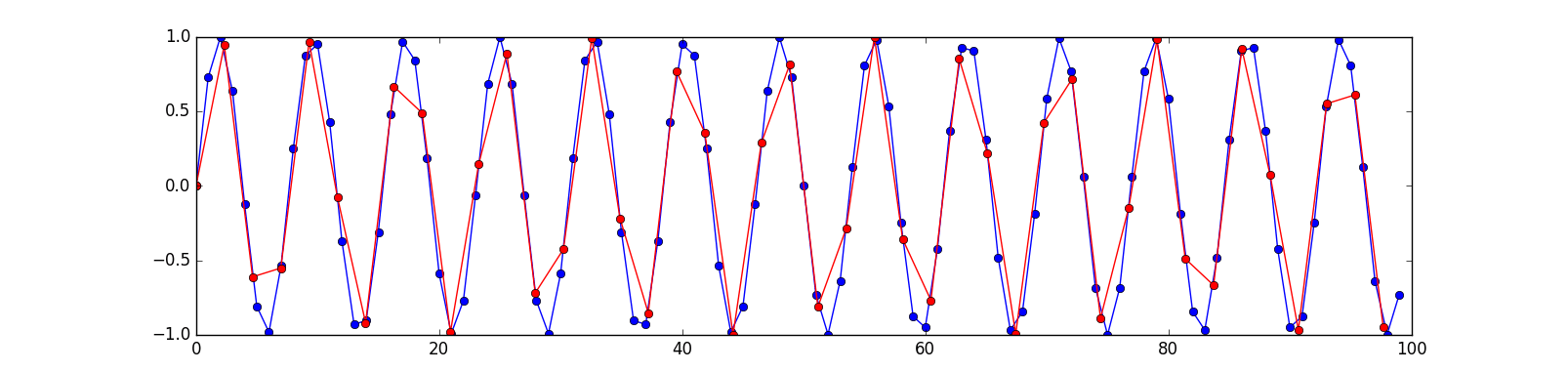
Построение данных является хорошим первым шагом при проверке. Здесь я сделал правильный сюжет с точками, соединенными линиями. Эти строки полезны, поскольку они дают представление о том, где, как вы ожидаете, лежат данные с пониженной выборкой, а также подчеркивают, что данные с пониженной выборкой отсутствуют. (Это также будет работать, чтобы показать только линии для исходных данных, но линии, как на графике ствола, слишком запутанные, imho.)

import numpy as np
import matplotlib.pyplot as plt # For ploting
from scipy import signal

fs = 100 # sample rate
rsample=43 # downsample frequency
fTwo=13 # frequency of the signal
x = np.arange(fs, dtype=float)
y = np.sin(2*np.pi*fTwo * (x/fs))
print y
f_res = signal.resample(y, rsample)
xnew = np.linspace(0, 100, f_res.size, endpoint=False)
#
# ##############################
#
plt.figure()
plt.plot(x, y, 'o')
plt.plot(xnew, f_res, 'or')
plt.show()

Несколько заметок:

Если вы пытаетесь создать общий алгоритм, используйте не округленные числа, в противном случае вы могли бы легко вводить ошибки, которые не отображаются, когда вещи даже кратны. Точно так же, если вам нужно увеличить масштаб для проверки, перейдите к нескольким случайным местам, а не, например, только к началу.

Обратите внимание, что я изменился fTwo быть значительно меньше, чем количество образцов. Так или иначе, вам нужно как минимум более одной точки данных на одно колебание, если вы хотите понять это.

Я также удаляю цикл для расчета y: в общем, вы должны попытаться векторизовать вычисления при использовании numpy.

Answer 2

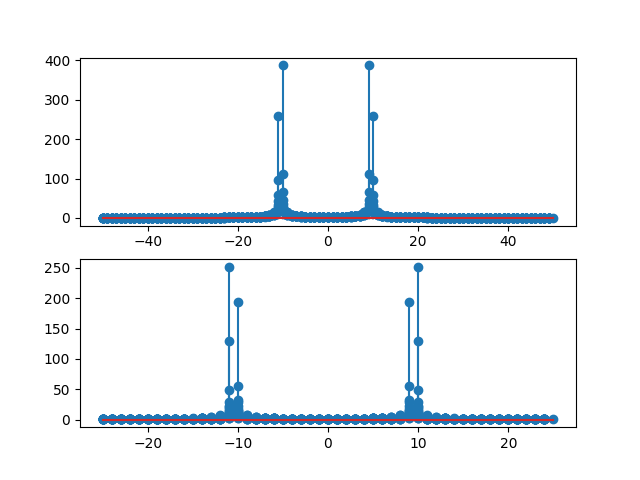
Спектр пересэмплированного сигнала должен иметь тон на той же частоте, что и входной сигнал, только в меньшей полосе частот Найквиста.

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import scipy.fftpack as fft


fs = 100 # sample rate
rsample=50 # downsample frequency
fTwo=10 # frequency of the signal

n = np.arange(1024)
y = np.sin(2*np.pi*fTwo/fs*n)
y_res = signal.resample(y, len(n)/2)

Y = fft.fftshift(fft.fft(y))
f = -fs*np.arange(-512, 512)/1024
Y_res = fft.fftshift(fft.fft(y_res, 1024))
f_res = -fs/2*np.arange(-512, 512)/1024

plt.figure(1)
plt.subplot(211)
plt.stem(f, abs(Y))
plt.subplot(212)
plt.stem(f_res, abs(Y_res))
plt.show()

Тон все еще в 10.

Answer 3

Если вы сэмплируете сигнал, оба сигнала будут иметь одно и то же значение и заданное время, так что просто прокрутите "время" и убедитесь, что значения одинаковы. В вашем случае вы выбираете частоту дискретизации от 100 до 50. Предполагая, что у вас есть данные за 1 секунду для построения вашего x из fs, затем просто выполните циклы от t = 0 до t = 1 с шагом 1/50 и убедитесь, что что Yd(t) = Ys(t), где Yd d - пониженная частота f, а Ys - исходная частота выборки. Или просто сказать, что Yd(n) = Ys(2n) для n = 1,2,3,...n=total_samples-1.