Расчет коэффициентов отделимого состояния

Question

Учитывая отделяемое состояние 2-кубита

φ = φ₀ ⊗ φ₁

с

φ_i= a_i0| 0> + a_i1| 1>

φ, таким образом, можно записать как

φ = b₀₀| 00> + b₀₁| 01> + b₁₀| 10> + b₁₁| 11>

с

b_ij = a_0i a_1j.

---

Теперь давайте дадим некоторое b_ij, т.е. произвольное состояние 2-кубита

φ = b₀₀| 00> + b₀₁| 01> + b₁₀| 10> + b₁₁| 11>

Пусть B = (b_ij). По разложению Шмидта существуют 2x2 матрицы U, V, Σ, такие что

• U, V унитарный

• Σ положительная полуопределенная диагональ

• B = U ∘ Σ ∘ V*

Пусть σ₀, σ₁ - два диагональных элемента из Σ.

Состояние φ = b₀₀| 00> + b₀₁| 01> + b₁₀| 10> + b₁₁| 11> запутано тогда и только тогда, когда σ₀ + σ₁ > 1.

---

ВОПРОС

Для заданного состояния φ = b₀₀| 00> + b₀₁| 01> + b₁₀| 10> + b₁₁| 11> и его разложения Шмидта B = U ∘ Σ ∘ V*, такого что σ₀ + σ₁ ≤ 1 т.е. состояние отделимо. Это означает, что существуют φ_i= a_i0| 0> + a_i1| 1>, так что φ можно записать в виде

φ = φ₀ ⊗ φ₁

Как рассчитать A = (a_ij) из B = (b_ij), т.е. из U, V, Σ?

Это обратная сторона

b_ij = a_0i a_1j

учитывая, что b_ij определяет отделимое состояние.

Answer 1

Если вам дано чистое состояние и обещано, что оно отделимо, вам не нужно разложение Шмидта для вычисления частей. Просто положите амплитуды в сетку, считайте пропорции между столбцами для одной части и считайте пропорции между строками для другой.

То есть утверждение, что 2-кубитная система φ отделима, так что φ = αβ гарантирует, что φ₀₀/φ₀₁ = φ₁₀/φ₁₁ = β₀/β₁ и что φ₀₀/φ₁₀ = φ₀₁/φ₁₁ = α₀/α₁. И знание α₀ / α₁ достаточно, чтобы решить для α, за исключением глобального фазового фактора. (Примечание: работайте с пропорциями α₀:α₁ вместо соотношений α₀ / α₁, если α₁ может быть нулевым.)

Это обобщает на системы с большим количеством кубитов. Данное подмножество кубитов является отделимым тогда и только тогда, когда группировка по всем остальным кубитам дает вам набор частей с согласованными пропорциями между их частями. И пропорции между частями ограничивают все, кроме глобального фазового фактора.

Использование разложения Шмидта в качестве ярлыка

Разложение Шмидта действительно облегчает это. Он выполняет всю тяжелую работу по "восстановлению пропорций". Если чистая система отделима, то ее разложение SVD должно иметь только одно ненулевое сингулярное значение, и это сингулярное значение должно равняться 1. Таким образом, у вас есть что-то вроде:

  |1 0 0 ...|
U |0 0 0 ...| V
  |0 0 0 ...|
  |... . ...|

Но это просто умножение первого столбца U на первый ряд V! Итак, у нас есть система с n * m записями, которая создается из системы с n записями и системой с m записями... Да, первый столбец и первая строка содержат амплитуды α и β.

пример

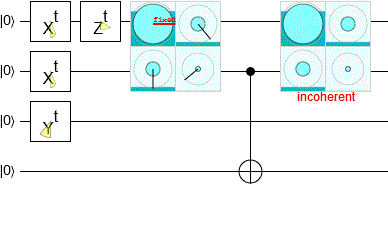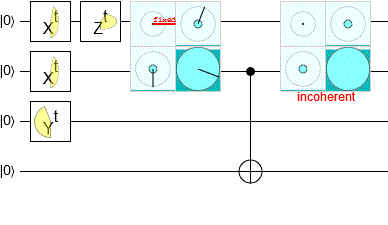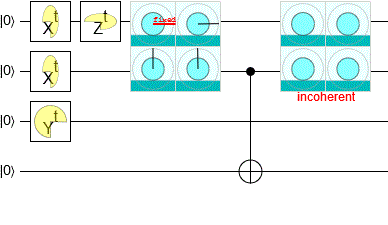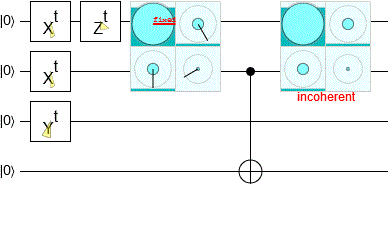
В моем симуляторе схем Quirk есть встроенные индикаторы амплитуды, которые выполняют такое разделение (без использования SVD). Вы можете увидеть код, который делает это на github, хотя он полностью основан на GPU, так что не очень понятно.

(Это был самый сложный экран для записи, так как он должен выполнить группировку, а затем сравнить все группы. Но некоторые группы могут не иметь амплитуды, поэтому их следует игнорировать, и в системе могут возникать помехи из-за ошибок с плавающей запятой. так что вы должны сосредоточиться на больших группах и... blergh.)

Также вы можете играть с ним в самом симуляторе. Вот пример схемы, использующей эти дисплеи:

Вы также можете найти этот пост в блоге интуитивно полезным.