Численный метод Рунге-Кутты Плохое приближение
Я пытаюсь использовать метод Рунге-Кутты, чтобы сравнить его с функцией lsode. Но он работает довольно плохо, все остальные методы, которые я использовал (Фовардс и Эйлер, Хеун) для сравнения с lsode, делают работу лучше, до такой степени, что они почти неотличимы от lsode.
Это то, что мой код возвращает 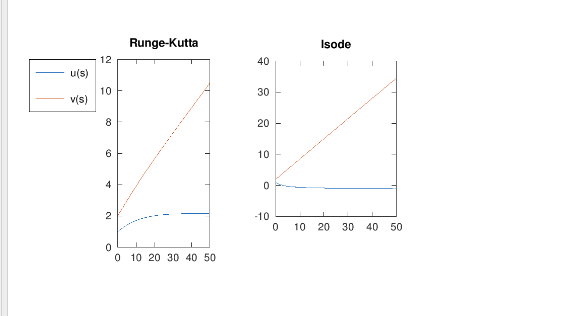
Если кто-то может указать способ улучшить его или если я делаю что-то не так, я был бы признателен.
Вот что я использую для метода Рунге-Кутты
%Initial conditions
u(1) = 1;
v(1) = 2;
p(1) = -1/sqrt(3);
q(1) = 1/sqrt(3);
%Graf interval / step size
s0 = 0;
sf = 50;
h = 0.25;
n=(sf-s0)/h;
s(1) = s0;
%-----------------------------------------------------------------------%
for j = 2:n
i = j-1;
k1_u(j) = p(i);
k1_v(j) = q(i);
k1_p(j) = (-2*v(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1);
k1_q(j) = (-2*u(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1);
u1(j) = p(i) + (1/2)*k1_u(j)*h;
v1(j) = q(i) + (1/2)*k1_v(j)*h;
p1(j) = (-2*v(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1) + (1/2)*k1_p(j)*h;
q1(j) = (-2*u(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1) + (1/2)*k1_q(j)*h;
k2_u(j) = p1(j);
k2_v(j) = q1(j);
k2_p(j) = (-2*v1(j)*p1(j)*q1(j)) / (u1(j)*u1(j) + v1(j)*v1(j) + 1);
k2_q(j) = (-2*u1(j)*p1(j)*q1(j)) / (u1(j)*u1(j) + v1(j)*v1(j) + 1);
u2(j) = p(i) + (1/2)*k2_u(j)*h;
v2(j) = q(i) + (1/2)*k2_v(j)*h;
p2(j) = (-2*v(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1) + (1/2)*k2_p(j)*h;
q2(j) = (-2*u(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1) + (1/2)*k2_q(j)*h;
k3_u(j) = p2(j);
k3_v(j) = q2(j);
k3_p(j) = (-2*v2(j)*p2(j)*q2(j)) / (u2(j)*u2(j) + v2(j)*v2(j) + 1);
k3_q(j) = (-2*u2(j)*p2(j)*q2(j)) / (u2(j)*u2(j) + v2(j)*v2(j) + 1);
u3(j) = p(i) + k3_u(j)*h;
v3(j) = q(i) + k3_v(j)*h;
p3(j) = (-2*v(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1) + k3_p(j)*h;
q3(j) = (-2*u(i)*p(i)*q(i)) / (u(i)*u(i) + v(i)*v(i) + 1) + k3_q(j)*h;
k4_u(j) = p3(j);
k4_v(j) = q3(j);
k4_p(j) = (-2*v3(j)*p3(j)*q3(j)) / (u3(j)*u3(j) + v3(j)*v3(j) + 1);
k4_q(j) = (-2*u3(j)*p3(j)*q3(j)) / (u3(j)*u3(j) + v3(j)*v3(j) + 1);
s(j) = s(j-1) + h;
u(j) = u(j-1) + (h/6)*(k1_u(j) + 2*k2_u(j) + 2*k3_u(j) + k4_u(j));
v(j) = v(j-1) + (h/6)*(k1_v(j) + 2*k2_v(j) + 2*k3_v(j) + k4_v(j));
p(j) = p(j-1) + (h/6)*(k1_p(j) + 2*k2_p(j) + 2*k3_p(j) + k4_p(j));
q(j) = q(j-1) + (h/6)*(k1_q(j) + 2*k2_q(j) + 2*k3_q(j) + k4_q(j));
endfor
subplot(2,3,1), plot(s,u);
hold on; plot(s,v); hold off;
title ("Runge-Kutta");
h = legend ("u(s)", "v(s)");
legend (h, "location", "northwestoutside");
set (h, "fontsize", 10);
1 ответ
Вы неправильно поняли что-то в методе. Промежуточные значения для p,q рассчитываются так же, как промежуточные значения для u,vи оба являются "шагами Эйлера" с последними вычисленными уклонами, а не отдельными вычислениями уклонов. Для первых это
u1(j) = u(i) + (1/2)*k1_u(j)*h;
v1(j) = v(i) + (1/2)*k1_v(j)*h;
p1(j) = p(i) + (1/2)*k1_p(j)*h;
q1(j) = q(i) + (1/2)*k1_q(j)*h;
Расчет для k2 Значения тогда правильные, следующие средние точки должны быть правильно вычислены с помощью "шагов Эйлера" и т. д.