Ошибка интеграции deSolve ODE, я использую неправильную функцию?

Question

Я пытаюсь решить систему уравнений, связанных с биологическими процессами. Одно уравнение (около 5) предназначено для фармакокинетической (ФК) кривой формы C = Co(exp(k1*t)-exp(k2*t). Необходимо одновременно решить производную этого уравнения вместе с некоторыми уравнениями связывания ферментов и исходными результатами, которые не соответствуют ожидаемым. После устранения неполадок понял, что производная PK не интегрируется численно сама по себе, если k отрицательно, используя функцию desolve ode. Я пробовал все методы (lsode, lsoda и т. Д.) В функции ode, но безуспешно. Попробовал настроить rtol, не решается.

Есть ли альтернатива функции deSolve ode, которую я должен изучить? Или другой способ решить эту проблему?

Ниже приведен код с упрощенным уравнением для демонстрации проблемы. Когда k отрицательно, интегрированное решение не соответствует аналитическому результату. Когда k положительно, результаты ожидаются.

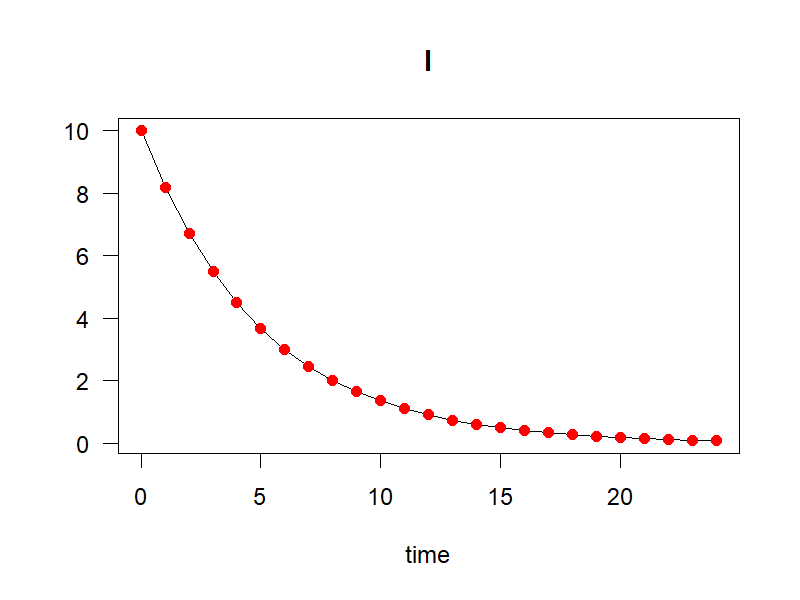
Первое изображение, результат с k = 0,2: аналитические и интегрированные результаты совпадают, когда k положительно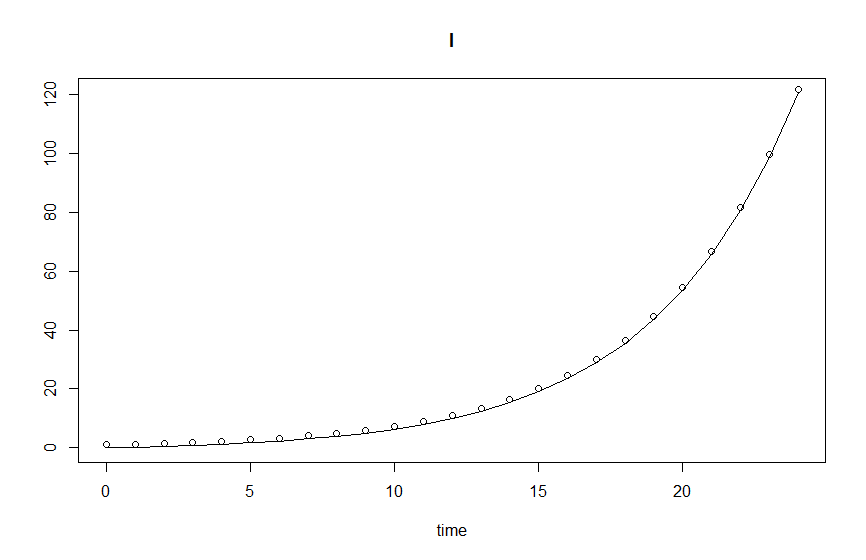

Второе изображение, результат с k = -0,2: интегрированный результат не соответствует аналитическому, когда k отрицательно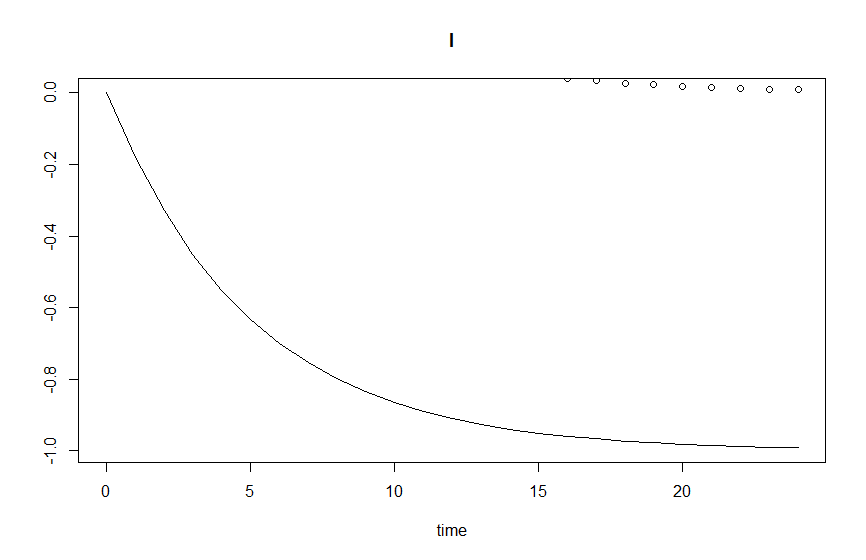

      library(deSolve)

abi <- function(t, state, parameters) {
    with(as.list(c(state, parameters)), {
        
        dI <- k*exp(k*t)
                list(c(dI))
    })
}

k <- c(-0.2)

times <- seq(0, 24, by = 1)

I_analytical <- exp(k*times)

parameters <- c(k)
state <- c(I = 0)

out <- ode(y = state, times = times, func = abi, parms = parameters)

plot(out)
points(I_analytical ~ times)

Было отмечено, что начальное условие легко разрешает приведенный выше пример, что очень полезно. Вот уравнение, которое я не могу точно интегрировать. Я безуспешно пробовал несколько разных начальных условий.

      library(deSolve)

## Chaos in the atmosphere
CYP <- function(t, state, parameters) {
    with(as.list(c(state, parameters)), {
        #dE <- ksyn - (kdeg * E) + (k2 * EI) - (k1 * E * I)
        #dEI <- (k1 * E * I) - (k2 * EI) + (k4 * EIstar) - (k3 * EI)
        #dEIstar <- (k3 * EI) - (k4 * EIstar)
        #dOcc <- dEI + dEIstar
        dI <- a*tau1*exp(tau1*t) + b*tau2*exp(tau2*t) + c*tau3*exp(tau3*t)
            #list(c(dE, dEI, dEIstar, dOcc, dI))
          list(c(dI))
    })
}

ifit <- c(-0.956144311,0.82619445,0.024520276,-0.913499862,-0.407478829,-0.037174745)
a = ifit[1]
b = ifit[2]
c = ifit[3]
tau1 = ifit[4]
tau2 = ifit[5]
tau3 = ifit[6]


parameters <- c(ksyn = 0.82, kdeg = 0.02, k1 = 2808, k2 = 370.66, k3 = 2.12, k4 = 0.017, a, b, c, tau1, tau2, tau3)

#state <- c(E = 41, EI = 0, EIstar = 0, Occupancy = 0, I = 0.0)
state <- c(I=-0.01)
times <- seq(0, 24, by = .1)
out <- ode(y = state, times = times, func = CYP, parms = parameters)

I_analytical <- a*exp(tau1*times) + b*exp(tau2*times) + c*exp(tau3*times)

plot(out)
points(I_analytical ~ times)

Целевая кривая и линия решения оды.

Answer 1

Начальное значение должно быть

      state <- c(I= a + b + c)
#state <- c(I = 1)

Answer 2

Первый сценарий содержит несколько проблем. Наиболее важные два из них заключаются в том, что (1) модельная функция ( ) должен содержать производную, а не интегрированную функцию, в то время как (2) аналитически интегрированная модель пропустила I_0, который является результатом постоянной интегрирования.

Предположим, что модель распада первого порядка

dI / dt = k I

то аналитическое интегрирование дает

I_t = I_0 exp(узлы)

Тогда код будет таким:

      library(deSolve)

abi <- function(t, state, parameters) {
  with(as.list(c(state, parameters)), {
    # dI <- k*exp(k*t) # original
    dI <-  k * I       # corrected, should be the dervivative
    list(c(dI))
  })
}

k <- -0.2 # simplified, c() was not necessary
times <- seq(0, 24, by = 1)

# correction: set I0 to a value > zero
I0 <- 10

# I_analytical <- exp(k*times)    # original
I_analytical <- I0 * exp(k*times) # corrected, multiplied with I0

#state <- c(I = 0) # original
state <- c(I = I0) # corrected
parameters <- c(k = k)

out <- ode(y = state, times = times, func = abi, parms = parameters)

plot(out)
points(I_analytical ~ times)

При желании этот код можно упростить.