Mathcad to Matlab - тестирование белого шума, FFT и NPS

Question

Mathcad to Matlab - тестирование белого шума, FFT и NPS

Я пытаюсь написать простую функцию в Matlab для расчета и построения спектра мощности шума (NPS). Прежде всего я хотел проверить, был ли алгоритм, который я получил от моего учителя, был в порядке, и все. Вот оно (сделано в mathcad)

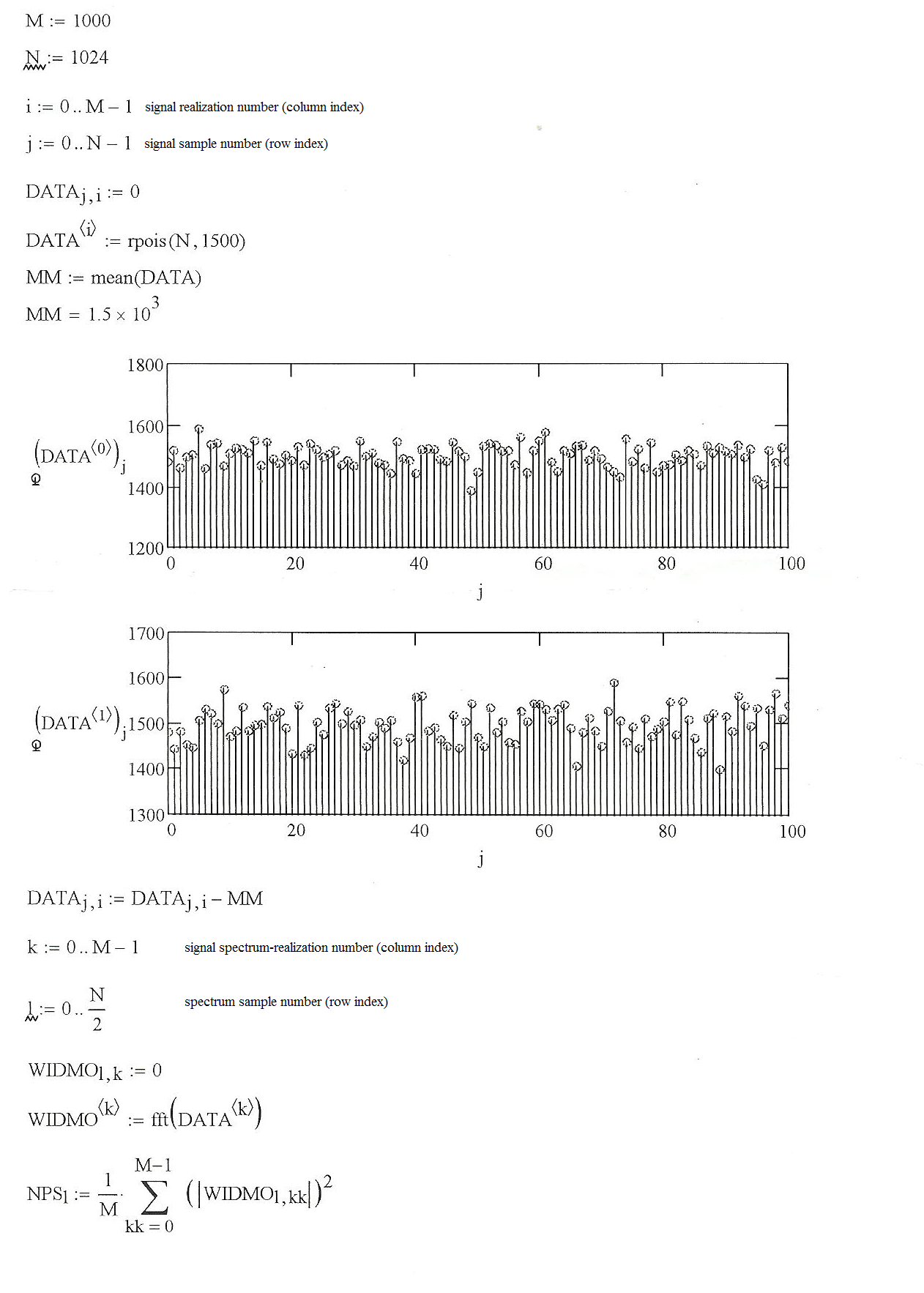
Поэтому я попытался скопировать и вставить его в скрипт Matlab и в итоге получил следующий код:

clear all;
clc;


N=1000;
O=1024;
mn=zeros(N,O);
n0=1500;
s=sqrt(n0);
W=zeros(N,O/2);
W1=zeros(N,O);

for k=1:N
    for l=1:O
        mn(k,l)=n0+round(sin(randn)*s);
    end
end

for k=1:N
    for l=1:O
        mn(k,l)=mn(k,l)-n0;
    end
end

for k=1:N
    W1(k,:)=fft(mn(k,:));
end

for k=1:N
   for l=1:O/2
       W(k,l)=W1(k,l);
   end
end

NPS1=(abs(W)).^2;
NPS2=sum(NPS1);
NPS=(1/N)*NPS2;

plot(NPS);

Я не использую распределение Пуассона, и я переключил индексы строк-столбцов, но это не должно иметь значения (верно?). Проблема в том, что значения на моем графике в 400 раз больше, чем ожидалось.

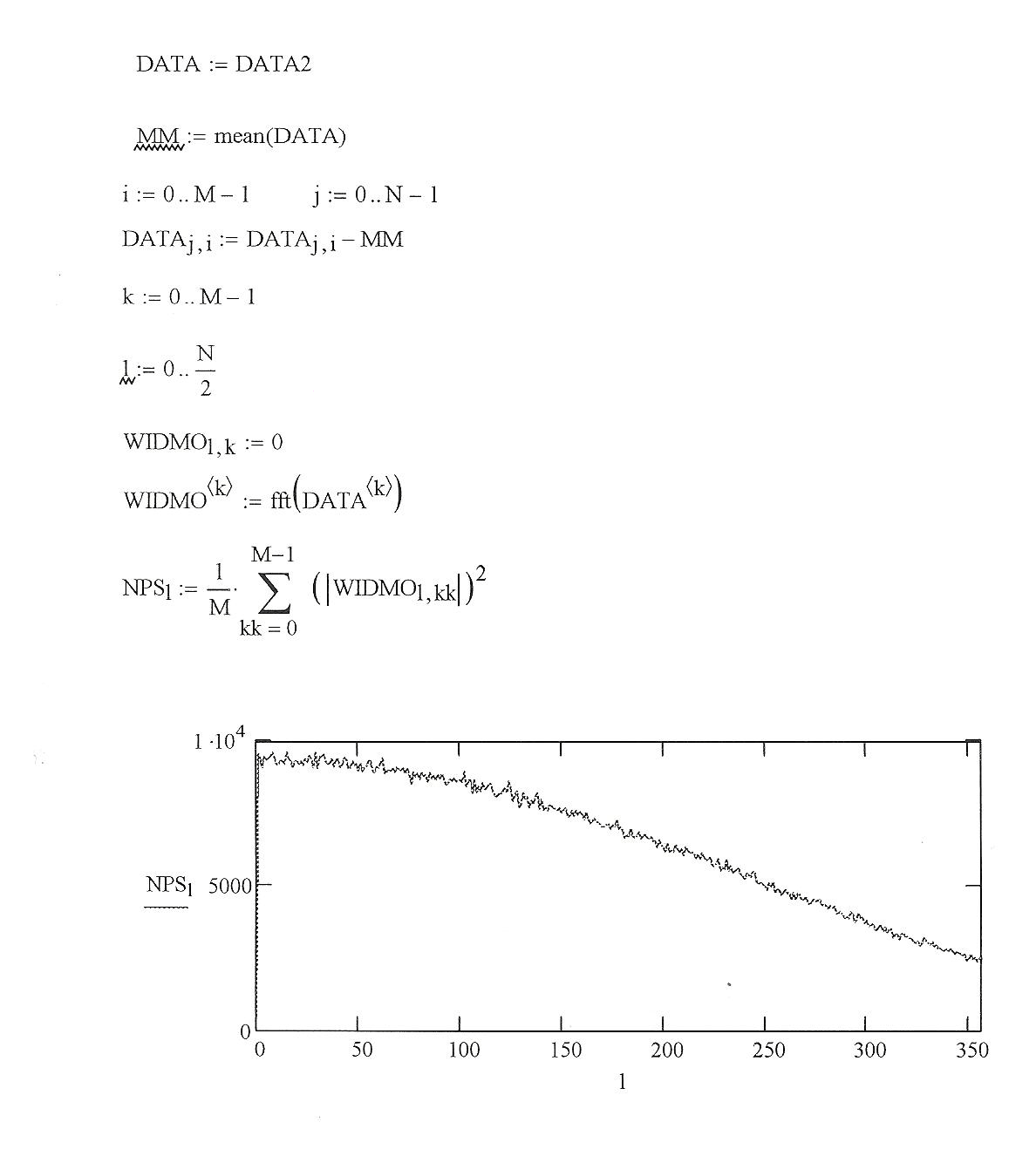
Вот как это должно выглядеть:

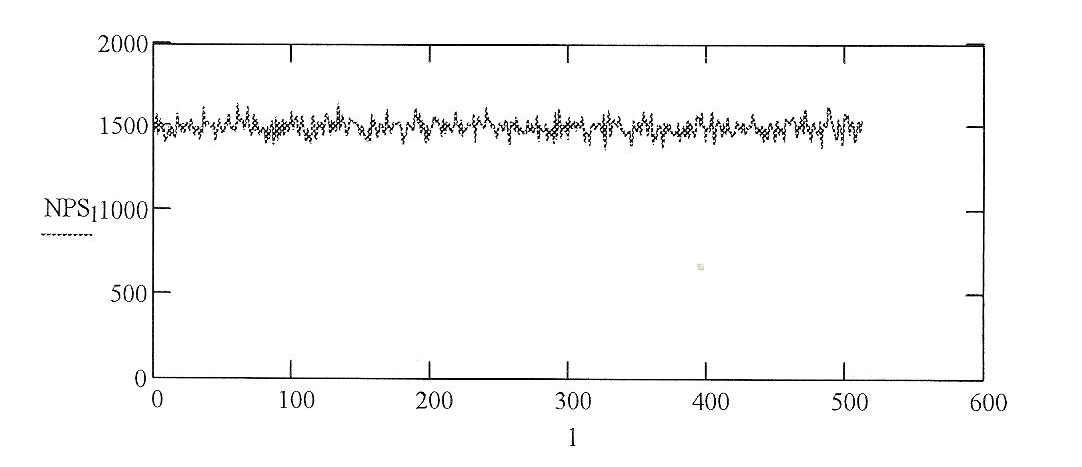
Я пытался выяснить, что я сделал не так, но после некоторого времени тестирования некоторых изменений я вернулся на круги своя... Единственное, что меня беспокоит, так это то, что, возможно, функция Matlab fft работает несколько иначе, чем та, которая использовалась в Mathcad (не могу сказать, что я понимаю это полностью). Любая добрая душа может сказать мне, если речь идет о функции FFT? Или я просто слепой тупой, который не видит глупой ошибки, которую он совершил? Приветствия и извините за мой плохой английский.

[РЕДАКТИРОВАТЬ]

Через некоторое время мой учитель попросил меня проверить, работает ли этот метод с коррелированным (своего рода) шумом, как он работает (опять же) в mathcad. После корреляции его NPS должен "падать" на более высоких частотах. Проблема в том, что это не так. Код, который я использую для проверки, выглядит следующим образом:

clear all;
clc;

N=1000;

mn = poissrnd(N, N, N);
dataw=zeros(N);

for k=1:N ## loop used for my teacher's correlation method
    for l=1:N
        if l>1 && l<N
            dataw(k,l)=dataw(k,l)+mn(k,l)*0.5+mn(k,l-1)*0.25+mn(k,l+1)*0.25;
        elseif l==1
            dataw(k,l)=dataw(k,l)+mn(k,l)*0.75+mn(k,l+1)*0.25;
        else
            dataw(k,l)=dataw(k,l)+mn(k,l)*0.75+mn(k,l-1)*0.25;
        end
    end
end

dataw = dataw - mean(dataw(:));
W1 = (1/sqrt(N))*fft(dataw, [], 1);

NPS1=(abs(W1)).^2;
NPS2=sum(NPS1);
NPS=(1/N)*NPS2;

plot(NPS);

Единственные изменения, которые я сделал в коде, исправленном rayryeng, - это квадрат матрицы шума (1000x1000), а также среднее значение 1000 и использование целого преобразованного вектора W1 вместо его "половины". Я знаю, что это сработало для моего учителя, но это не для меня... Есть ли что-то еще в matlab fft, которое я пропустил, или это "метод корреляции", который я использовал?

Добавим, как это выглядит в Mathcad после нескольких быстрых изменений (несколько небольших различий, но в целом это показывает эффект, который я должен получить). Он обрезал начало сканирования, но это точно то же самое, что я поставил в начале этого поста.

[EDIT2]

НВМ, это была просто проблема размерности в функции FFT. После изменения в fft(dataw, [], 2) это выглядит лучше.

2

matlab fft noise spectrum mathcad

Источник

user4354529 12 дек '14 в 17:54

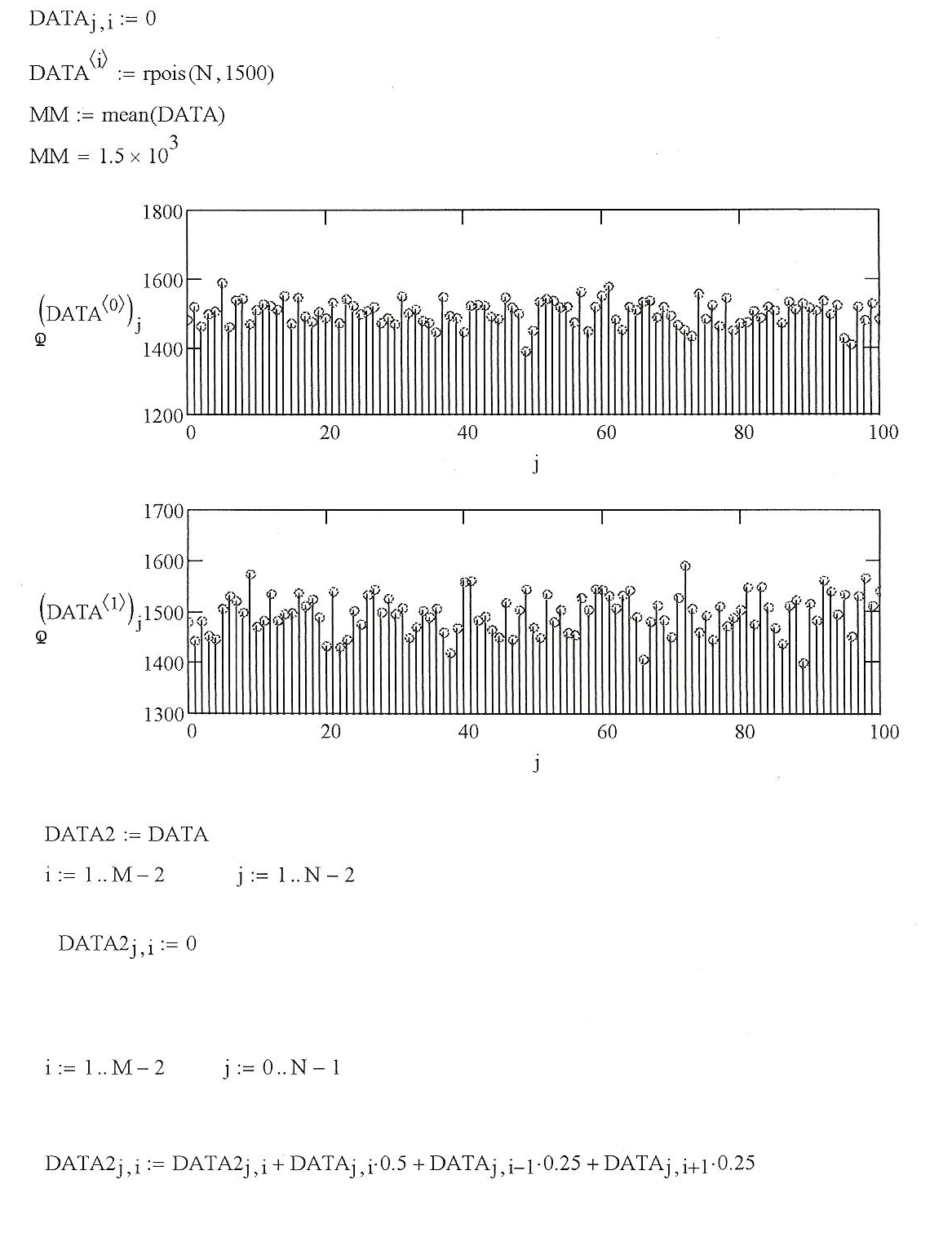
1 ответ

Решение

Другие вопросы по тегам matlab fft noise spectrum mathcad

user3250829 12 дек '14 в 18:30 2014-12-12 18:30 · Accepted Answer · 2014-12-12 18:30

Основная причина, по которой это не работает, связана с коэффициентом масштабирования FFT между MathCad и MATLAB. С MathCad существует дополнительный коэффициент масштабирования 1/sqrt(N) тогда как MATLAB не включает этот упомянутый коэффициент масштабирования. Таким образом, вам нужно будет умножить результаты FFT на этот коэффициент масштабирования, если вы хотите имитировать результаты, которые вы видите с помощью MathCad.

Кроме того, у меня есть несколько предложений с вашим кодом:

Мы можем полностью сделать это векторизованным без каких-либо петель
Функции, такие как fft а также randn может работать с матрицами, и вы можете специально применить функцию к одному конкретному измерению.

Обратите внимание, что я заменил ваше распределение случайного шума на случайный шум Пуассона (из poissrnd), чтобы я мог имитировать результаты, полученные с вашим учителем.

По сути, ваш код может быть заменен на:

clear all;
clc;

N=1000;
O=1024;
n0=1500;
s=sqrt(n0);

%mn = round(sin(randn(N,O)*s));
mn = poissrnd(n0, N, O); %// CHANGE
mn = mn - mean(mn(:)); %// Remove mean
W1 = (1/sqrt(N))*fft(mn, [], 1); %// CHANGE FROM ABOVE
W = W1(:,1:O/2);

NPS1=(abs(W)).^2;
NPS2=sum(NPS1);
NPS=(1/N)*NPS2;

plot(NPS);

Обратите внимание, что вы добавили среднее значение 1500 при генерации случайных данных.... только для того, чтобы снова вычесть из них 1500 без какой-либо обработки данных смещения. Я только что удалил это из вашего кода для синусоидального округления случайного шума. Я оставил этот код закомментированным, потому что я не запускаю его сейчас в любом случае. Также обратите внимание, что randn может принимать количество строк и столбцов, чтобы вы могли генерировать случайную матрицу значений. Также, fft может работать над строками или столбцами и рассматривать каждый сигнал в этом измерении как одномерный сигнал. В этом случае вы хотите работать с каждым столбцом и обрабатывать над строками, поэтому мы указываем параметр 1 в качестве третьего параметра.

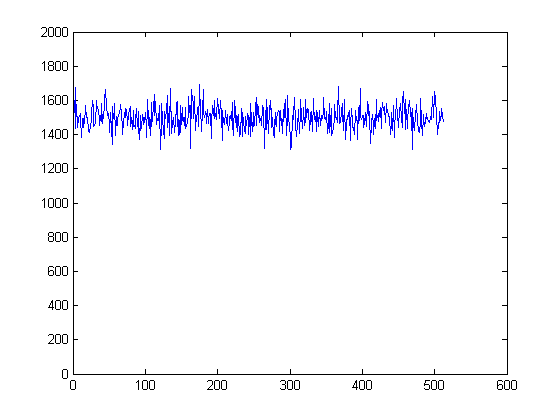
Это то, что мы получаем, когда я запускаю код выше:

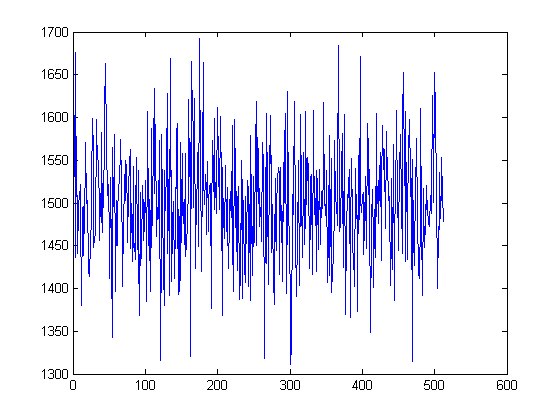
Вы видите, что оно колеблется около 1500, что мы и ожидали, когда мы взяли из случайного распределения Пуассона с lambda=1500, Если вы действительно хотите, чтобы график выглядел как ваш учитель, измените пределы оси Y с 0 на 2000 следующим образом:

ylim([0 2000]);

Таким образом, мы получаем: