IEEE 754: обоснование формата: субнормальные и нормальные числа

Question

Может кто-нибудь уточнить:

1. Почему именно формат субнормальных чисел ±(0.F) × 2^-126 и нет ±(1.F) × 2^-127?
2. Почему именно формат нормальных чисел такой: ±(1.F) × 2^exp а не, скажем, ±(11.F) × 2^exp, или, скажем, ±(10.F) × 2^exp?

Answer 1

Формат с плавающей запятой представляет числа, используя знак (- или +), показатель степени (целое число в некотором диапазоне от e _min до e _max включительно) и мантиссу, которая представляет собой число из p цифр в основании b , где b - это фиксированная база для формата, а p называется точностью. Мы будем рассматривать двоичный формат, в котором b равно двум.

Пусть цифры _{мантиссы равны} f₀ , f ₋₁, f₋₂,… f_{1− p} , так что _{мантисса} равна сумме _−p<i≤0 f_i• b ⁱ , а представленное значение равно (−1) ^s • b ^e • sum _−p<i≤0 f_i• b ⁱ , где s - бит для знака, а e - показатель степени.

Если f₀ равно нулю, мы можем опустить его из суммы, и представленное значение равно (−1) ^s • b ^e • sum _{−p<i≤−1} f_i• b ⁱ = (−1) ^s • b ^{e −1}• сумма _{−p<i≤−1} f_i• b ⁱ⁺¹ = (−1) ^s • b ^{e −1}• сумма _{1− p <i≤0} f_i−1• b ⁱ. Следовательно, когда f₀ равно нулю, а e не является e_мин , есть два представления числа. Кодирование их обоих было бы расточительным, поэтому нам нужна схема кодирования, которая не кодирует оба представления.

Мы добиваемся этого:

• Некоторое значение E кодирует показатель степени e . Значения s и от f ₋₁ до f _{1− p} хранятся непосредственно в виде битов.
• Если E равно нулю, e равно e _min, а f₀ равно нулю.
• Если E не равно нулю, e - это E - смещение, а f₀ - это единица, где смещение равно 1 - e _min .
• (Специальное значение E может быть зарезервировано для представления бесконечностей и NaN, здесь не обсуждается.)

Это представление и эта схема кодирования отвечают на вопросы:

Почему именно субнормальные числа имеют формат ±(0.F) × 2 ^{- 126,} а не ±(1.F) × 2 - ¹²⁷?

Субнормальные числа в форме ±(1.F) × 2 ⁻¹²⁷ не будут включать ноль и будут включать числа, не входящие в представленные числа формата, так как они будут иметь числа с ненулевыми цифрами, меньшими, чем у младших ненулевых цифр. нулевая цифра в выбранном наборе. (Самая низкая цифра формы, описанной в первом абзаце, соответствует b ^{e _min +(1− p )} , тогда как числа в форме ±(1.F) × 2 ⁻¹²⁷ будут иметь младшую цифру, соответствующую b ^{e _min - 1+(1− п )}.)

Почему именно формат нормальных чисел таков : ±(1.F) × 2 ^exp, а не, скажем, ±(11.F) × 2^exp , или, скажем, ±(10.F) × 2^exp?

Где десятичная точка (или «точка счисления») находится в значении, не имеет значения, пока она фиксирована. Представление, описанное с использованием десятичной точки сразу после первой цифры, как используется здесь, эквивалентно представлению с использованием десятичной точки после последней цифры или в любой другой позиции с подходящей корректировкой границ экспоненты: тот же набор чисел является Представленные и арифметические свойства идентичны. Итак, рассматривая разницу между 1.F и 11.F, нам все равно, где находится десятичная точка. Однако нас действительно волнует, сколько цифр представлено. Формат с плавающей запятой использует представление с фиксированным числом цифр. 11.F имеет на одну цифру больше, чем 1.F, и у нас нет причин кодировать это.

Что касается разницы между 11.F и 10.F, причина, по которой существует различие между нормальным и субнормальным, заключается в том, что арифметически существует два представления одного и того же числа, если первая цифра равна нулю, а показатель степени не является минимальным. Определение одной формы как нормальной позволяет нам устранить эти повторяющиеся представления. Однако 11.F и 10.F представляют собой разные числа, поэтому нет никаких дубликатов, которые нужно исключать, и нет причин говорить, что одно из них является нормальным, а другое - нет.

Answer 2

Я проверил свойства обоих форматов на упрощенном примере. Для простоты я использую форматы и, где F имеет 2 десятичные цифры и нет ±.

Минимальные (ненулевые) / максимальные значения:

      Format          Min value (non-zero)           Max value
0.F × 10^-2     0.01 × 10^-2 = 0.0001          0.99 × 10^-2 = 0.0099
1.F × 10^-3     1.00 × 10^-3 = 0.001           9.99 × 10^-3 = 0.00999

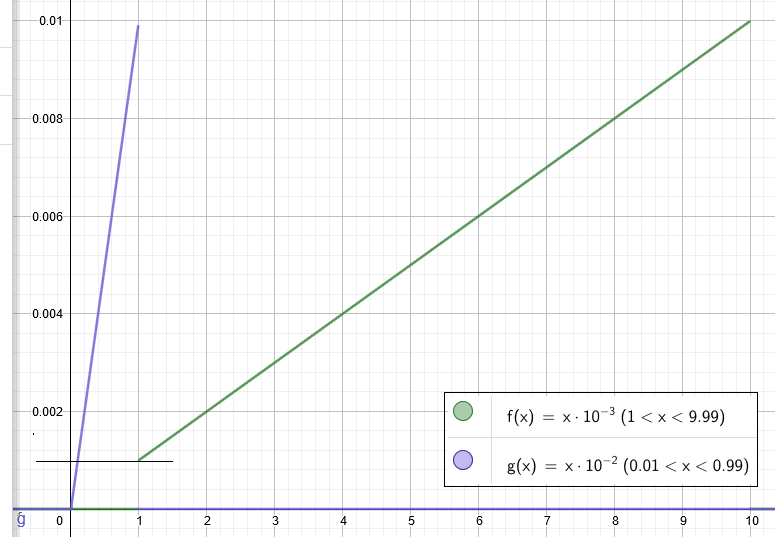
Вот графическое представление:

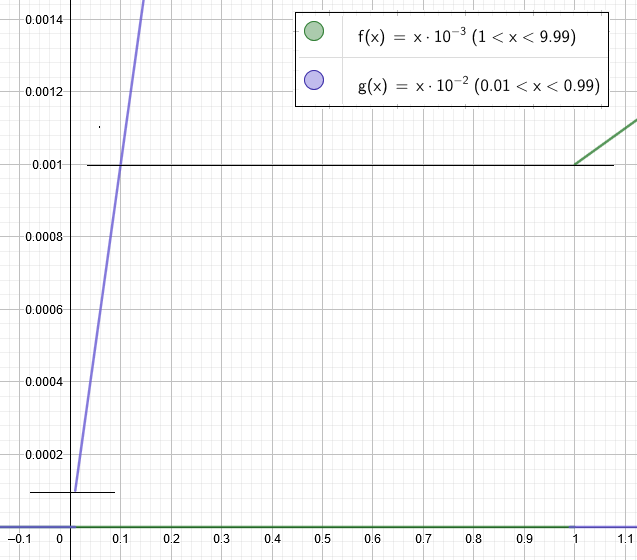
Здесь мы видим, что начиная со значения 0.001формат больше не позволяет представлять меньшие значения. Однако формат позволяет представлять меньшие значения. Вот увеличенная версия:

Вывод: из графического представления мы видим, что свойства формата 0.F × 10^-2 по формату 1.F × 10^-3 находятся:

1. дает больший динамический диапазон: log10(max_real / min_real): 1.99 vs 0.99
2. дает меньшую точность: может быть представлено меньше значений: 100 vs 900

Похоже, что для субнормалов предпочтительнее IEEE 754. more dynamic range несмотря на less precision. Следовательно, формат субнормальных чисел таков: ±(0.F) × 2^-126 и нет ±(1.F) × 2^-127.