Стандартизация вектора в R, чтобы значения сдвигались к границам

Question

У меня есть вектор следующим образом -

      a <- c(0.211, 0.028, 0.321, 0.072, -0.606, -0.364, -0.066, 0.172, 
-0.917, 0.062, 0.117, -0.136, -0.296, 0.022, 0.046, -0.19, 0.057, 
-0.625, -0.01, 0.158, 0.407, -0.328, -0.347, -0.512, -0.101, 
0.008, -0.406, -0.014, 0.517, 0.085, -0.525, -0.635, -0.603, 
-0.105, 0.643, -0.094, -0.26, 0.348, -0.106, 0.608, 0.146, -0.343, 
-0.537, -0.661, 0.166, -0.037, -0.224, -0.269, -0.221, -0.623, 
-0.025, 0.382, 0.201, -0.281, -0.699, -0.373, -0.146, -0.273, 
-0.354, -0.138, -0.098, 0.312, 0.467, 0.156, 0.264, -0.108, -0.707, 
-1, -0.423, -0.708, -0.235, -0.219, -0.645, 0.081, 0.704, -0.639, 
0.368, -0.578, 0.158, -0.04, -0.071, -0.125, 0.006, 0.423, 0.112, 
1, 0.373, -0.554, -0.092, 0.509, -0.535, -0.619, -0.31, -0.082, 
-0.367, -0.574, 0.029, 0.391, 0.062, -0.476)

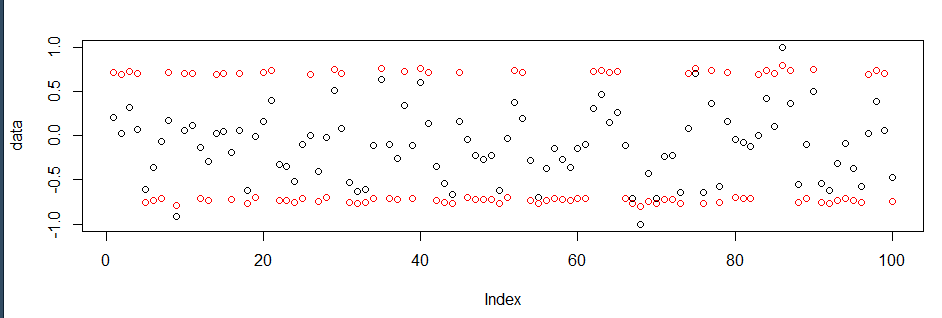
Диапазон этого вектора составляет от -1 до 1, и это выглядит так -

> plot(a)

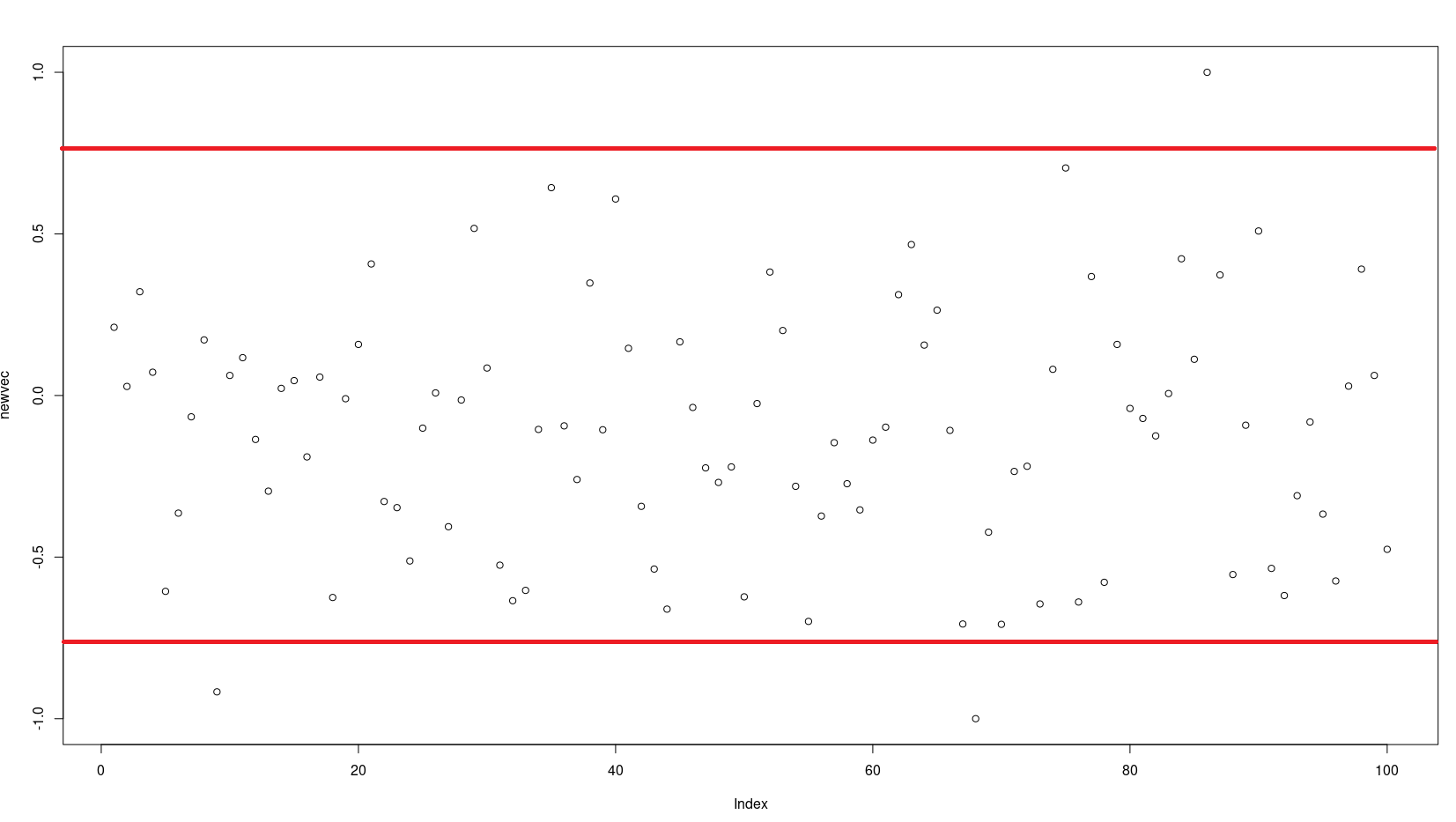Есть ли способ стандартизировать вектор aчтобы все значения уходили от нуля и сдвигались в сторону 1 или -1? (возле красных линий).

Было бы здорово, если бы я мог контролировать степень того, насколько эти значения могут приближаться к 1 или -1.

Answer 1

Вы можете использовать минимальную и максимальную стандартизацию. Обычно min max std. используется для масштабирования значений от 0 до 1. Однако вы можете масштабировать значения до любого диапазона [a, b], используя следующее уравнение:

      X_Scaled = a + (x - min(x)) * (b-a) / (max(x) - min(x))

Итак, в вашем случае, давайте разберемся на два шага.

Во-первых: вы хотите, чтобы положительные значения были сосредоточены вокруг, а отрицательные значения - вокруг -0.75. Таким образом, мы можем просто отфильтровать значения в ваших данных.

      data <- runif(100, -1, 1)

positive_vals <- data[data > 0]
negative_vals <- data[data < 0]

Второй шаг: вы хотите контролировать, насколько они приблизятся к этому значению. Таким образом, вы можете определить диапазон и центр. Скажем, ряд 0.05 и центр дает нам a = 0.7 и b=0.8, верно? Мы можем сделать то же самое с отрицательным центром.

      range <- 0.05
upper_center <- 0.75
lower_center <- -0.75

b1 <- upper_center + range
a1 <- upper_center - range

b2 <- lower_center + range
a2 <- lower_center - range

Наконец, мы применяем уравнение min-max для обоих случаев, заботясь о сохранении исходных позиций положительных и отрицательных значений в исходном массиве.

      # normalize them using, say, min-max
positive_vals <- a1 + ((positive_vals - min(positive_vals)) * (b1 - a1)) / (max(positive_vals) - min(positive_vals))
negative_vals <- a2 + ((negative_vals - min(negative_vals)) * (b2 - a2)) / (max(negative_vals) - min(negative_vals))

new_data <- data
new_data[data > 0] <- positive_vals
new_data[data < 0] <- negative_vals

# Plot the results!
plot(data)
points(new_data, col = "red")

Если вас не устраивает перемещение значений так близко к 0.75просто увеличьте range. Вы также можете переместить centers путем определения различных значений.

Используя предоставленные вами данные: