Реализация алгоритма Брон-Кербоша в python
Для проекта колледжа я пытаюсь реализовать алгоритм Брон-Кербоша, то есть перечислять все максимальные клики в данном графе.
Я пытаюсь реализовать первый алгоритм (без поворота), но мой код не дает всех ответов после тестирования его на примере Википедии, мой код до сих пор:
# dealing with a graph as list of lists
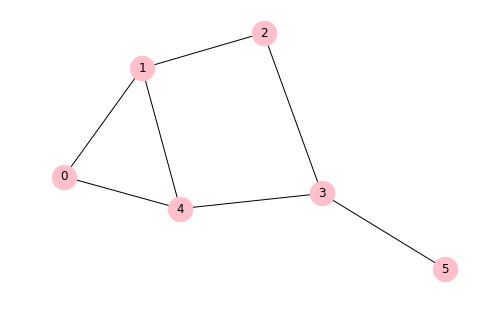
graph = [[0,1,0,0,1,0],[1,0,1,0,1,0],[0,1,0,1,0,0],[0,0,1,0,1,1],[1,1,0,1,0,0],[0,0,0,1,0,0]]
#function determines the neighbors of a given vertex
def N(vertex):
c = 0
l = []
for i in graph[vertex]:
if i is 1 :
l.append(c)
c+=1
return l
#the Bron-Kerbosch recursive algorithm
def bronk(r,p,x):
if len(p) == 0 and len(x) == 0:
print r
return
for vertex in p:
r_new = r[::]
r_new.append(vertex)
p_new = [val for val in p if val in N(vertex)] # p intersects N(vertex)
x_new = [val for val in x if val in N(vertex)] # x intersects N(vertex)
bronk(r_new,p_new,x_new)
p.remove(vertex)
x.append(vertex)
bronk([], [0,1,2,3,4,5], [])
Любая помощь, почему я получаю только часть ответа?
2 ответа
Python запутывается, потому что вы модифицируете список, по которому он перебирает.
+ Изменить
for vertex in p:
в
for vertex in p[:]:
это заставит его перебирать копию p вместо этого.
Вы можете прочитать больше об этом на http://effbot.org/zone/python-list.htm.
Как правильно указывает @VaughnCato, ошибка повторялась P[:], Я подумал, что стоит отметить, что вы можете "выдать" этот результат, а не распечатывать его следующим образом (в этом переработанном коде):
def bronk2(R, P, X, g):
if not any((P, X)):
yield R
for v in P[:]:
R_v = R + [v]
P_v = [v1 for v1 in P if v1 in N(v, g)]
X_v = [v1 for v1 in X if v1 in N(v, g)]
for r in bronk2(R_v, P_v, X_v, g):
yield r
P.remove(v)
X.append(v)
def N(v, g):
return [i for i, n_v in enumerate(g[v]) if n_v]
In [99]: list(bronk2([], range(6), [], graph))
Out[99]: [[0, 1, 4], [1, 2], [2, 3], [3, 4], [3, 5]]
В случае, если кто-то ищет реализацию алгоритма Брон-Кербоша в будущем...
Реализация двух форм алгоритма Брон-Кербоша из Википедии:
Без поворота
алгоритм BronKerbosch1(R, P, X) равен,
если P и X оба пусты, то:
сообщить R как максимальную клику
для каждой вершины v в P do
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P:= P \ {v}
X:= X ⋃ {v}
adj_matrix = [
[0, 1, 0, 0, 1, 0],
[1, 0, 1, 0, 1, 0],
[0, 1, 0, 1, 0, 0],
[0, 0, 1, 0, 1, 1],
[1, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0]]
N = {
i: set(num for num, j in enumerate(row) if j)
for i, row in enumerate(adj_matrix)
}
print(N)
# {0: {1, 4}, 1: {0, 2, 4}, 2: {1, 3}, 3: {2, 4, 5}, 4: {0, 1, 3}, 5: {3}}
def BronKerbosch1(P, R=None, X=None):
P = set(P)
R = set() if R is None else R
X = set() if X is None else X
if not P and not X:
yield R
while P:
v = P.pop()
yield from BronKerbosch1(
P=P.intersection(N[v]), R=R.union([v]), X=X.intersection(N[v]))
X.add(v)
P = N.keys()
print(list(BronKerbosch1(P)))
# [{0, 1, 4}, {1, 2}, {2, 3}, {3, 4}, {3, 5}]
С поворотом
алгоритм BronKerbosch2(R, P, X) :
если P и X оба пусты, то
сообщает R как максимальную клику
выберите опорную вершину u в P ⋃ X
для каждой вершины v в P \ N (u):
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P:= P \ {v}
X:= X ⋃ {v}
import random
def BronKerbosch2(P, R=None, X=None):
P = set(P)
R = set() if R is None else R
X = set() if X is None else X
if not P and not X:
yield R
try:
u = random.choice(list(P.union(X)))
S = P.difference(N[u])
# if union of P and X is empty
except IndexError:
S = P
for v in S:
yield from BronKerbosch2(
P=P.intersection(N[v]), R=R.union([v]), X=X.intersection(N[v]))
P.remove(v)
X.add(v)
print(list(BronKerbosch2(P)))
# [{0, 1, 4}, {1, 2}, {2, 3}, {3, 4}, {3, 5}]