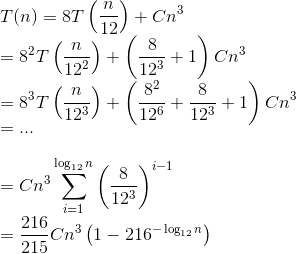Оценка сложности рекурсивной функции

Question

void f(int n) {
    if (!n) return;
    for (int i=0; i<8; i++)
        f(n/12);
    g(n,3);
}

void g(int n, int i) {
    if (!i) return;
    for (int j=n; j>0; --j) {
        g(n,i-1);
    }
}

Я пытаюсь оценить сложность этой функции. Вот как я это делаю:

1. Оцените данную сложность. Это зависит от значения i, и каждая запись поднимает n записей цикла, поэтому вся сложность равна Θ(n^3).
2. Теперь, начиная с ф. T(n) = 8*(T/12) + g(n, 3). Теперь применяем основную теорему. log8(12) < 3 (степень сложности f), поэтому вся сложность f равна Θ(n^3).

Это правильное решение или мне нужно рассмотреть что-то еще?

Answer 1

Поскольку T(n) заканчивается, когда n = 0рекурсия T должно быть log12(T) глубокий (игнорирование округления и выключения и т. д.)

Если мы расширим серию, учитывая ваш результат для g:

Второе слагаемое в скобках исчезающе мало, поэтому его можно игнорировать. Таким образом, общая сложность Θ(n^3),