Подсчет всех четных чисел в b-дереве в Прологе

Я хочу написать программу на Прологе, которая создает список всех четных целых чисел, которые находятся в b-дереве. Это то, что я написал до сих пор. Предикат, который считает все элементы в дереве. Я не знаю, где поцарапать.

Domains
element=integer
tree=a(tree,element,tree);void
    list=integer*

Predicates
     nondeterm count(tree,element)
     nondeterm count_even(tree,list)

Clauses
    count(a(void,Number,void),1).
count(a(Esq,_,Dreta),Counter) :-
    count(Esq,Counter1),
    count(Dreta,Counter2),
    Counter=Counter1+Counter2+1.

Goal
       count(a(a(void,1,void),5,a(a(void,4,void),1,a(void,4,void))),N).

Большое спасибо.

Источник

2 ответа

Решение

Не знаю ничего о Visual Prolog, но в обычном Prolog я бы сделал что-то вроде следующего...

Во-первых, я бы обозначил пустое дерево как атом btree и представляют непустое дерево как структуру арности 3, таким образом:

btree( Payload, LeftChildren, RightChildren )

где Payload это данные для узла (очевидно, целое число), с LeftChildren а также RightChildren будучи btrees, представляющими соответственно левого и правого потомков текущего узла.

Обход дерева для подсчета этих узлов с четными узлами очень прост. Открытый предикат имеет арность 2, принимая структуру [bound] btree, которую нужно исследовать, и привязанное или несвязанное значение, представляющее количество четных элементов. Он вызывает внутренний рекурсивный предикат-помощник, который обходит дерево и вырабатывает счет.

count_even( T , N ) :- count_even( T , 0 , N ) .

Внутренний предикат также прост. Имея арность 3, первый аргумент - это дерево, которое нужно исследовать, второй - накопитель, а третий - окончательный счет (который не будет объединен до самого конца). Есть два возможных случая.

  1. Если дерево пустое, у нас есть окончательный счет:

    count_even( btree , N , N ) .

  2. Если дерево не пустое, мы проверяем текущий узел, а затем рекурсивно обходим левые и правые дочерние деревья, таким образом:

    count_even( btree( V , L , R ) , T , N ) :-
  is_even( V , X ) ,
  T1 is T+X ,
  count_even( L , T1 , T2 ) ,
  count_even( R , T2 , N  )
  .

Нам также нужен простой помощник, чтобы сообщить нам, является ли конкретное значение четным или нечетным:

is_even( V , 1 ) :- 0 is V mod 2 , ! .
is_even( V , 0 ) .

Следует отметить, что используемая вами структура данных сама по себе не является b-деревом: это двоичное дерево.

B-деревья представляют собой обобщение двоичного дерева с сбалансированной высотой, оптимизированного для хранения на диске. Каждый узел имеет переменное количество ключей и переменное количество дочерних элементов (соответствующее количеству ключей). Для получения дополнительной информации см.

Вот изображение B-дерева:

Визуализация B-Tree

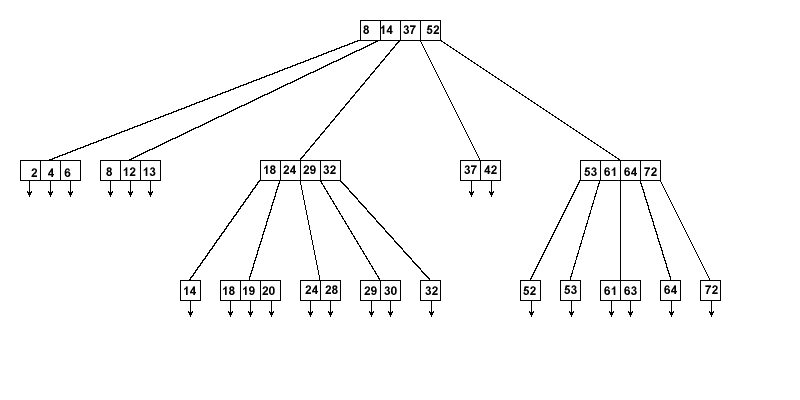
И изображение бинарного дерева:

Визуализация двоичного дерева

Источник

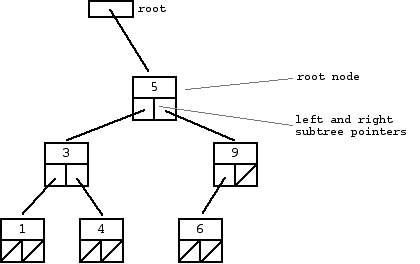
Вы должны проверить каждый узел, чтобы увидеть, является ли он четным или нечетным, и считать только те, которые являются четными. Простое изменение вашей программы должно сделать (однако я бы сделал это немного по-другому):

element=integer
tree=a(tree,element,tree);void
    list=integer*

Predicates
     nondeterm count_even(tree,list)

Clauses
    count_even(a(void,Number,void),Value):-
      Value = 1 - Number mod 2.
count_even(a(Esq,Number,Dreta),Counter) :-
    count_even(Esq,Counter1),
    count_even(Dreta,Counter2),
    count_even=Counter1 + Counter2 + 1 - Number mod 2.

Я просто считаю 1 - Number mod 2 который равен 1, когда число четное, и 0 в противном случае.

Источник
Другие вопросы по тегам