Минимальная циклическая подстрока в большей циклической строке
Я пытаюсь найти алгоритм, который кульд возвращает длину самой короткой циклической подстроки в большей циклической строке.
Циклическая строка будет определяться как объединение двух или более одинаковых строк, например, "abababab" или "aaaa"...
Теперь в заданной, например, строке T = "abbcabbcabbcabbc" есть цикл шаблона "abbc", но самой короткой циклической подстрокой будет "bb".
2 ответа
Если вы просто ищете подстроку, которая появляется более одного раза:
Постройте суффикс-дерево из строки.
При создании дерева суффиксов вы можете рассчитывать повторные вхождения каждой подстроки и сохранять их по числу вхождений на узле.
Затем просто выполните BFS-поиск по дереву (который даст вам многоуровневый поиск, от более коротких до более длинных строк) и найдите первую подстроку длиной более 1, которая встречалась более одного раза.
Общая сложность: O (n) где n - длина строки
Редактировать:
Пути от корня до листьев имеют отношение один к одному с суффиксами S
Вы можете реализовать дерево, в котором каждый узел содержит одну букву, что обеспечит вам лучшую детализацию и позволит вам увидеть все подстроки по длине.
Вот суффиксное дерево банана, где каждый узел содержит одну букву, вы можете видеть, что у вас есть все подстроки.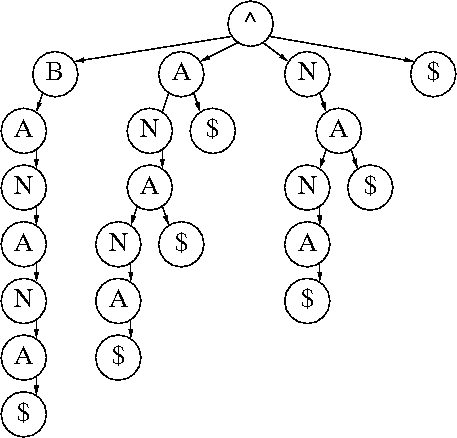
Если вы посмотрите на раздел приложений дерева суффиксов, вы увидите, что оно используется именно для такого рода задач - поиска вещей о подстроках.
Посмотрите на изображение из корня, вы можете увидеть ВСЕ подстроки, начинающиеся с корня (список BFS):
b
a
n
ba
an
na
ban
ana
nan
bana
anan
nana
banan
anana
banana
Позвольте мне вызвать "abbc" генератор в вашем примере - то есть строку, которую вы повторяете, чтобы получить большую строку.
Самое первое наблюдение состоит в том, что меньшая строка должна быть сделана повторением некоторой подстроки дважды.
Понятно, что наименьшая строка должна быть меньше генератора, повторяемого дважды (генератор 2*), потому что генератор 2* является циклическим.
Теперь обратите внимание, что вам нужно учитывать только строку, полученную генератором 3 раза, при поиске циклической строки меньшего размера. Действительно, если наименьшего нет, но оно есть в генераторе 4*, то оно должно охватывать как минимум два генератора, но тогда оно не будет самым маленьким.
Итак, теперь давайте предположим, что большая строка - генератор 3* (или генератор 2*). Также ясно, что если генератор имеет только разные цифры, то ответ - генератор 2*. Если нет, то вам просто нужно найти все пары одинаковых символов в большей строке, скажем, в позициях i и j, и проверить, является ли строка, начинающаяся с ai длиной 2*(ji), циклической. Если вы попробуете их в порядке увеличения джи, то вы можете остановиться после первого успеха.