Удалить значения за пределы кривой Лёсса

Я ищу, чтобы удалить выбросы, прежде чем применить модель. Я использую кривую Лёсса, чтобы разграничить линию тренда и установить границы выбросов. Я хотел бы удалить строки, которые находятся за пределами установленных ограничений. Помимо выполнения этой функции с помощью пользовательской функции, которая берет каждую точку по одному и проверяет локальный наклон Лёсса и т. Д.... есть ли более простой способ?

Линия тренда Лесса с ограничениями (1.2

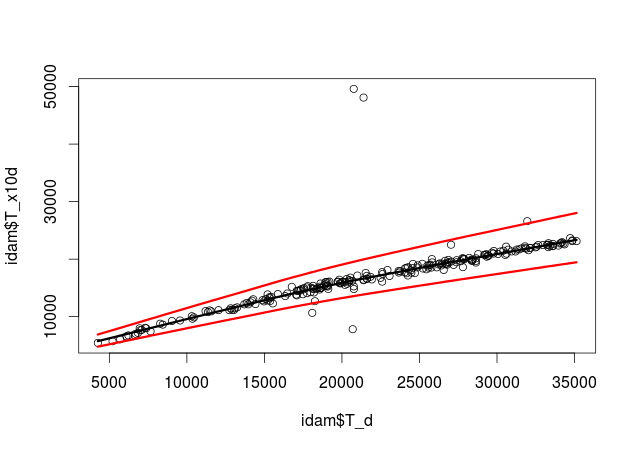
# Code generating image above
scatter.smooth( idam$T_d, idam$T_x10d)
loessline <- loess.smooth( idam$T_d, idam$T_x10d)
lines(loessline$x, loessline$y, lwd=3)
lines(loessline$x, loessline$y*1.2, lwd=3, col='red')
lines(loessline$x, loessline$y/1.2, lwd=3, col='red')
Источник

3 ответа

Решение

Обнаружение выбросов может быть сделано с помощью пакета DBSCAN R, хорошо известного алгоритма, используемого для идентификации кластера (см. WIKIPEDIA для более подробной информации).

Эта функция имеет три важных входа:

  • x: ваши данные (только числовое значение)
  • eps: максимальное расстояние цели
  • minPts: количество минимальных точек, чтобы рассматривать их как кластер

Оценка eps может быть выполнена с помощью функций knndist(...) и knndistplot(...):

  • knndistplot отобразит значения eps в вашем наборе данных для заданного k (т.е. minPts) ==> вы можете визуально выбрать эффективное значение eps (обычно в части кривой колена)
  • knndist оценит значения eps и вернет их в матрице из. вход k сгенерирует оценки 1:1:k, и вы можете использовать результат для программного определения точных значений eps & k

Далее вам нужно просто использовать dbscan(yourdata, eps, k) для получения объекта dbscan со следующими компонентами:

  • EPS: EPS, используемый для расчетов
  • minPts: минимальное количество баллов для идентификации кластера
  • cluster: целочисленный вектор, идентифицирующий точки, принадлежащие кластеру (= ​​1) или нет (=0). Последние соответствуют выбросам, которые вы хотите устранить.

Обратите внимание на следующие ограничения на dbscan:

  • dbscan использует евклидово расстояние, поэтому оно передается в "Проклятие измерений". Этого можно избежать с использованием PCA
  • dbscan устраняет наложенные точки, которые могут генерировать неопознанные точки. Эту проблему можно решить либо путем слияния результатов с вашими данными с помощью левого внешнего соединения, либо с помощью функции джиттера (...), которая добавляет шум к вашим данным. В соответствии с данными, которые вы отобразили, я думаю, что это может иметь место для ваших данных

зная эти ограничения, пакет dbscan предлагает два альтернативных метода: LOF и OPTICS (расширение DBSCAN)

Редактировать 25 января 2016

После ответа @rawr я привожу пример, основанный на mtcars набор данных, чтобы показать, как использовать dbscan для выявления выбросов. Обратите внимание, что мой пример будет использовать отличный data.table пакет вместо классического data.frame,

Сначала я начну копировать подход rawr для иллюстрации использования data.table

require(data.table)
require(ggplot2)
require(dbscan)
data(mtcars)
dt_mtcars <- as.data.table(mtcars)

# based on rawr's approach
plot(wt~mpg, data=dt_mtcars)
lo <- loess.smooth(dt_mtcars[,mpg], dt_mtcars[,wt])
lines(lo$x,lo$y, lwd=3)
lines(lo$x,lo$y * 1.2, lwd=3 , col=2 )
lines(lo$x,lo$y / 1.2, lwd=3 , col=2 )

введите описание изображения здесь

Таким образом, мы можем оценить, что получаем одинаковые результаты независимо от базовой поддержки.

Во-вторых, следующий код иллюстрирует подход DBSCAN, который начинается с определения eps а также k, необходимое количество баллов для идентификации кластера:

res_knn = kNNdist( dt_mtcars[, .(wt, mpg)] , k = 10)
dim_knn = dim(res_knn)
x_knn =  seq(1, dim_knn[1])
ggplot() + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 1])  , col = 1 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 2])  , col = 2 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 3])  , col = 3 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 4])  , col = 4 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 5])  , col = 5 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 6])  , col = 6 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 7])  , col = 7 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 8])  , col = 8 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 9])  , col = 9 ) ) + 
   geom_line( aes( x = x_knn , y = sort(res_knn[, 10]) , col = 10 ) )  +
   xlab('sorted results') + 
   ylab('kNN distance')

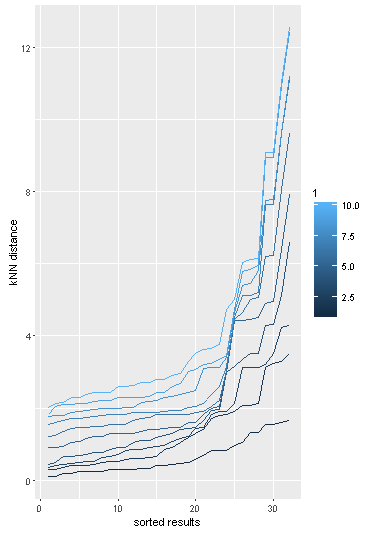
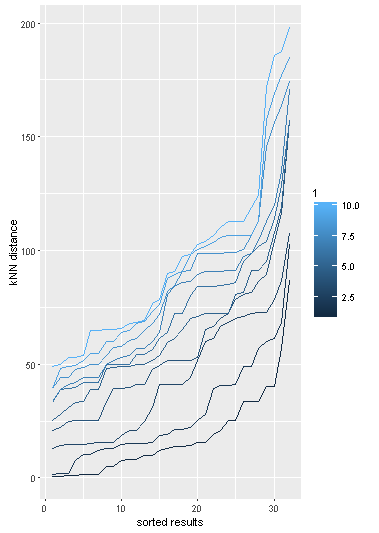
Результаты представлены в следующем графике:

введите описание изображения здесь

Это показывает, что рассчитанное расстояние кНН чувствительно к коэффициенту k Однако точный eps Значение для выделения выбросов находится в коленной части кривых ==> подходит eps расположен между 2 и 4. Это визуальная оценка, которая может быть автоматизирована с помощью соответствующих алгоритмов поиска (например, см. эту ссылку). относительно kнеобходимо определить компромисс, зная, что чем меньше k, тем менее строгие результаты.

В следующей части мы будем параметризовать dbscan с помощью eps = 3 (на основе визуальной оценки) и k = 4 за небольшие строгие результаты. Мы построим эти результаты с помощью кода rawr:

eps = 3
k = 4
res_dbscan = dbscan( dt_mtcars[, .(wt, mpg)] , eps , k )
plot(wt~mpg, data=dt_mtcars, col = res_dbscan$cluster)
lo <- loess.smooth(dt_mtcars[res_dbscan$cluster>0,mpg], dt_mtcars[res_dbscan$cluster>0,wt])
lines(lo$x,lo$y, lwd=3)
lines(lo$x,lo$y * 1.2, lwd=3 , col=2 )
lines(lo$x,lo$y / 1.2, lwd=3 , col=2 )

введите описание изображения здесь

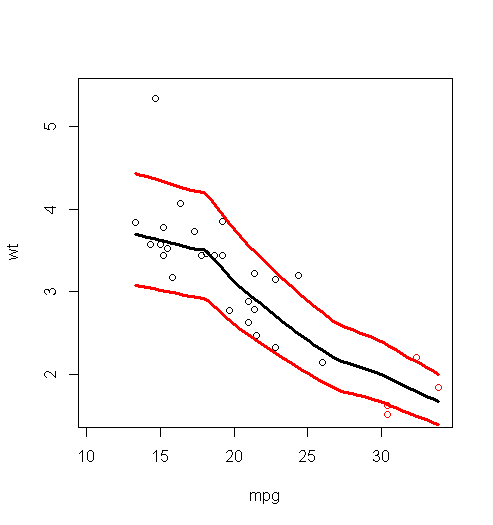
мы получили эту цифру, где мы можем оценить, что мы получили разные результаты от подхода Rawr, где точки, расположенные в mpg = [10,13] считаются выбросами.

Эти результаты могут рассматриваться как странные по сравнению с решением Rawr, которое работает в предположении наличия двумерных данных (Y ~ X). тем не мение mtcars является многомерным набором данных, где связь между переменными может быть (или не) линейной... Чтобы оценить эту точку, мы могли бы построить график этого набора данных, отфильтровав его по числовым значениям, например

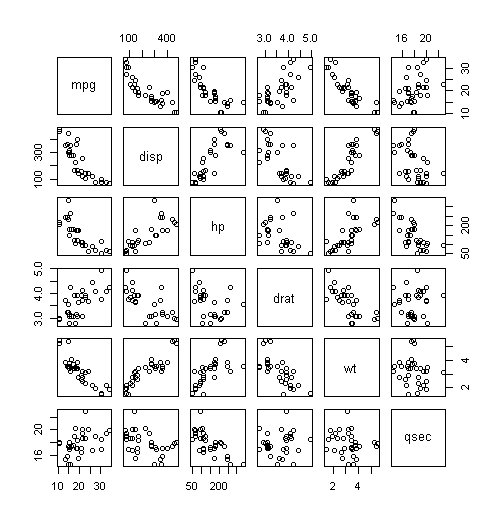
pairs(dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)])

введите описание изображения здесь

Если мы сосредоточимся только на результате wt ~ mpgМы могли бы подумать, что это антилинейные отношения на первый взгляд. Но с другими построенными отношениями это может быть не так, и найти выбросы в среде N-Dim немного сложнее. Действительно, одна точка может считаться выбросом при проецировании в конкретном двухмерном сравнении... но наоборот, если мы добавим новое измерение сравнения. Действительно, у нас может быть коллинеарность, которая может быть идентифицирована и, таким образом, укреплять кластерные отношения или нет.

Мои друзья, я согласен, что это много if и чтобы проиллюстрировать эту ситуацию, мы перейдем к dbscan анализ числовых значений mtcars,

Итак, я повторю процесс, представленный ранее, и давайте начнем с анализа расстояния kNN:

res_knn = kNNdist( dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)] , k = 10)
dim_knn = dim(res_knn)
x_knn =  seq(1, dim_knn[1])
ggplot() + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 1])  , col = 1 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 2])  , col = 2 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 3])  , col = 3 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 4])  , col = 4 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 5])  , col = 5 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 6])  , col = 6 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 7])  , col = 7 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 8])  , col = 8 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 9])  , col = 9 ) ) + 
    geom_line( aes( x = x_knn , y = sort(res_knn[, 10]) , col = 10 ) )  +
    xlab('sorted results') + 
    ylab('kNN distance')

отсортированные расстояния KNN

По сравнению с анализом, произведенным на wt ~ mpg, мы это видим kNNdist(...) производить гораздо более важное расстояние кНН (до 200 с k = 10 например). Однако у нас все еще есть часть колена, которая помогает нам оценить подходящий eps значение.

В следующей части мы будем использовать eps = 75 а также k = 5 а также

# optimal eps value is between 40 (k=1) and 130 (k=10)
eps = 75
k = 5
res_dbscan = dbscan( dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)] , eps , k )
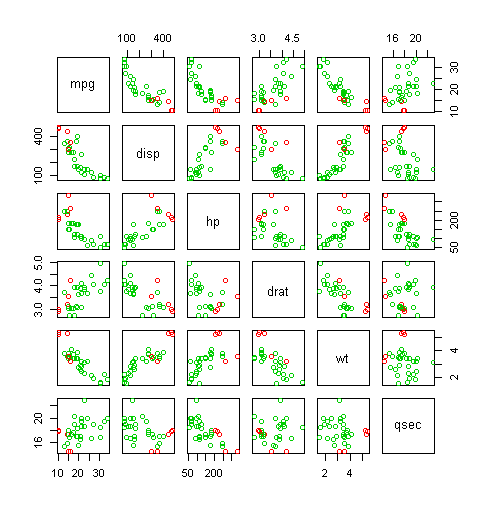
pairs(dt_mtcars[, .(mpg, disp, hp, drat, wt, qsec)] , col = res_dbscan$cluster+2L)

введите описание изображения здесь

Таким образом, график рассеяния этого анализа подчеркивает, что выявление выбросов может быть сложным в среде N-Dim из-за сложных отношений между переменными. Но обратите внимание, что в большинстве случаев выбросы расположены в угловой части 2D-проекции, что усиливает результаты, полученные при wt ~ mpg

Источник

Ты можешь использовать approxfun

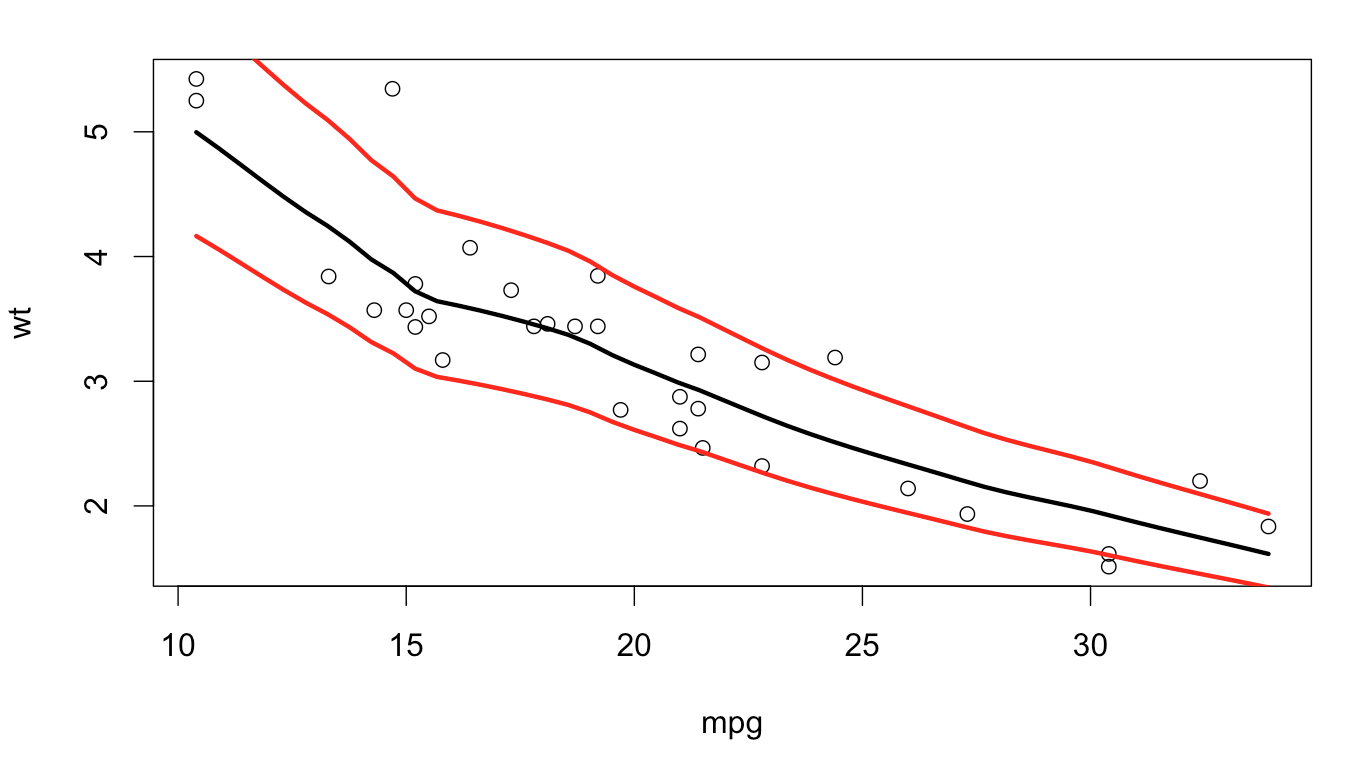
Вот пример с "выбросами"

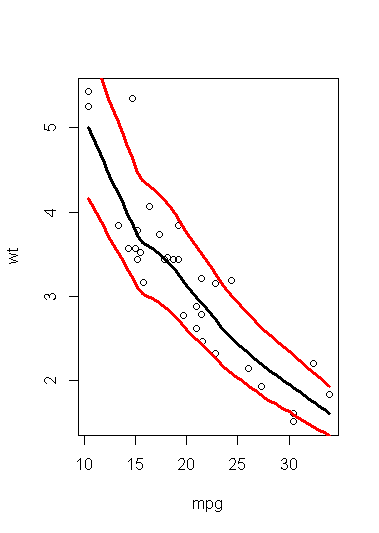
plot(wt ~ mpg, data = mtcars)
lo <- loess.smooth(mtcars$mpg, mtcars$wt)
lines(lo$x, lo$y, lwd = 3)
lines(lo$x, lo$y * 1.2, lwd = 3, col = 2)
lines(lo$x, lo$y / 1.2, lwd = 3, col = 2)

введите описание изображения здесь

approxfun возвращает функцию, используя наблюдаемые значения x, которые мы можем использовать для интерполяции набора новых значений y.

Затем вы можете установить порог для вызова точки выброса; здесь я использую 1.2 * y как и в оригинальном вопросе, для выявления экстремальных наблюдений.

f1 <- approxfun(lo$x, lo$y * 1.2)
(wh1 <- which(mtcars$wt > f1(mtcars$mpg)))
# [1]  8 17 18

f2 <- approxfun(lo$x, lo$y / 1.2)
(wh2 <- which(mtcars$wt < f2(mtcars$mpg)))
# [1] 28

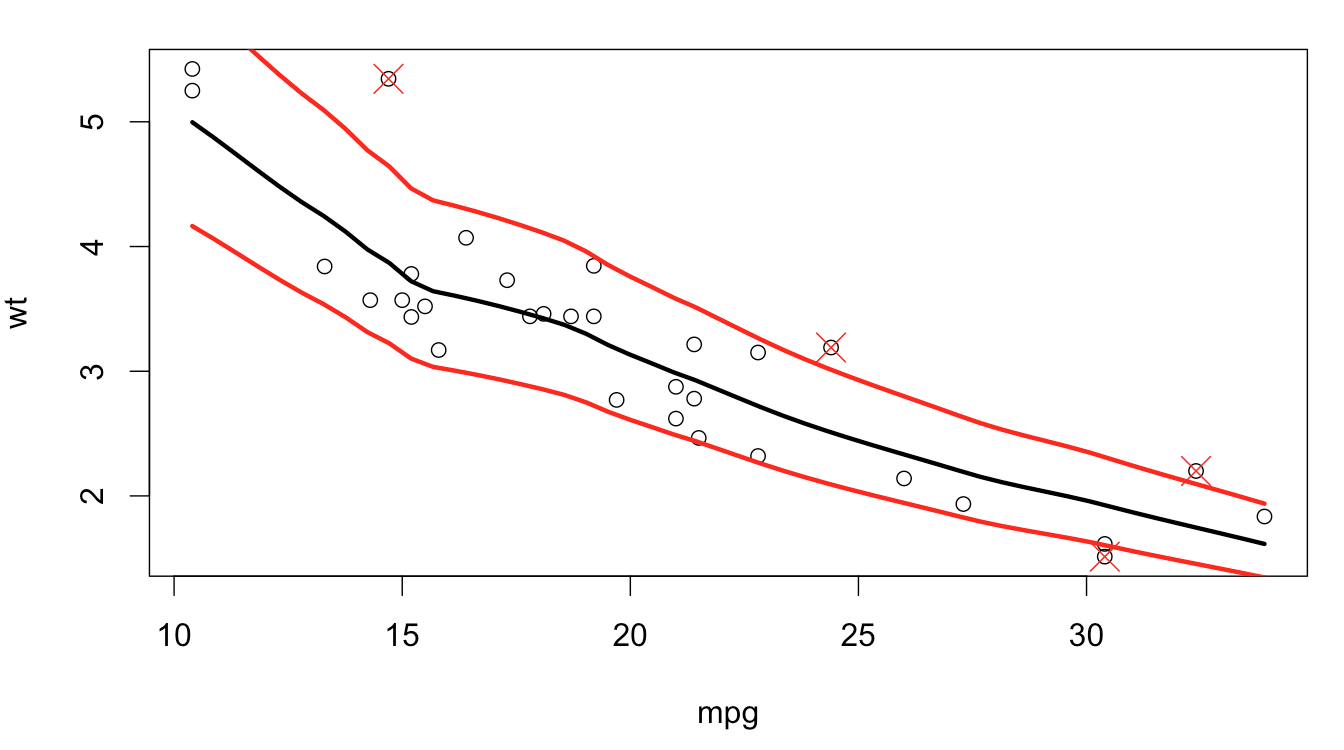
## identify points to exclude
mt <- mtcars[c(wh1, wh2), ]
points(mt$mpg, mt$wt, pch = 4, col = 2, cex = 2)

введите описание изображения здесь

## plot without points
plot(wt ~ mpg, data = mt2 <- mtcars[-c(wh1, wh2), ])
lo <- loess.smooth(mt2$mpg, mt2$wt)
lines(lo$x, lo$y, lwd = 3)
lines(lo$x, lo$y * 1.2, lwd = 3, col = 2)
lines(lo$x, lo$y / 1.2, lwd = 3, col = 2)

введите описание изображения здесь

Поскольку здесь есть пара шагов, вы можете упаковать это в функцию, чтобы немного упростить процесс:

par(mfrow = c(2,2))
with(mtcars, {
  plot_lo(mpg, wt)
  plot_lo(mpg, wt, limits = c(1 / 1.5, 1.5))
  dd <<- plot_lo(mpg, wt, limits = c(1 / 1.2, 1.2))
  plot_lo(mpg, wt, pch = 16, las = 1, tcl = .5, bty = 'l')
})

str(dd)
# List of 2
# $ x: num [1:28] 21 21 22.8 21.4 18.7 18.1 14.3 22.8 19.2 17.8 ...
# $ y: num [1:28] 2.62 2.88 2.32 3.21 3.44 ...

введите описание изображения здесь

plot_lo <- function(x, y, limits = c(-Inf, Inf), ...) {
  lo <- loess.smooth(x, y)
  fx <- approxfun(lo$x, lo$y * limits[1L])
  fy <- approxfun(lo$x, lo$y * limits[2L])

  idx <- which(y < fx(x) | y > fy(x))
  if (length(idx)) {
    x  <- x[-idx]
    y  <- y[-idx]
    lo <- loess.smooth(x, y)
  }

  op <- par(..., no.readonly = TRUE)
  on.exit(par(op))

  plot(x, y)
  lines(lo$x, lo$y, lwd = 3)
  lines(lo$x, lo$y * limits[1L], lwd = 3, col = 2L)
  lines(lo$x, lo$y * limits[2L], lwd = 3, col = 2L)

  invisible(list(x = x, y = y))
}
Источник

Мое предложение состоит в том, чтобы пойти посмотреть на outliers package, Этот пакет позволяет идентифицировать до анализа. Это очень простой пример:

library(outliers)
series<-c(runif(100,1,2),1000)
round(scores(series,prob=1,type="chisq"),3)

С помощью этой функции можно выполнить множество тестов, и вы можете установить уровень вероятности того, что вы чувствуете выброс, который вас устраивает.

series<-series[which(series<0.95),]
Источник
Другие вопросы по тегам