Как получить нетривиальное решение для этого граничного значения собственного порядка второго значения ODE?
ODE является y'' + lam * y(x)=0 с БК y'(0)-y(0)=0 а также y'(1)=0,
кленовый dsolve дает только тривиальное решение y(x)=0, Как можно попросить Maple дать нетривиальное решение, как это делает Mathematica по умолчанию?
Это то что я пробовал
ode:= diff(y(x),x$2)+ lambda*y(x)=0;
bc:=D(y)(0) - y(0)=0, D(y)(1)=0;
dsolve({ode,bc},y(x));
дает y(x)=0 на клене 2017.3 на windows 7.
Пока те же команды на Mathematica дают
ClearAll[y,x,lam];
DSolve[{y''[x]+lam y[x]==0,y'[0]-y[0]==0,y'[1]==0},y[x],x]
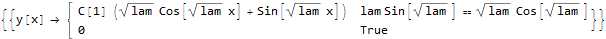
Что является правильным, вручную решая это.
У Maple есть отдельное граничное значение собственного значения dsolver? Нужен ли отдельный пакет? Я пытался помочь Maple, набрав assuming(lambda>0) но это не имело значения.
Я уверен, что Maple может сделать это, так как я знаю, что Maple очень силен в дифференциальных уравнениях, и мне просто нужна правильная опция или команда, чтобы сделать это.
1 ответ
Это не автоматически сгенерированный кусочный результат.
И второй звонок solve включает в себя решение для cos(lambda^(1/2)) а не простое имя. (Решение для lambda будет производить RootOf и иметь дело с любой заменой, которая кажется в лучшем случае неудобной.)
Но вот что-то. (Я ожидаю, что есть лучший способ...)
restart;
ans:=dsolve({diff(diff(y(x),x),x)+lambda*y(x) = 0,
D(y)(0)=K, D(y)(1) = 0},y(x)):
ans:=collect(ans,K); # for beauty's sake
/ 1/2 1/2 1/2 \
|sin(lambda x) cos(lambda ) cos(lambda x)|
ans := y(x) = |---------------- + -------------------------------| K
| 1/2 1/2 1/2 |
\ lambda lambda sin(lambda ) /
solve(eval(subs(x=0,y(0)=K,ans)),{K});
{K = 0}
eval(ans, %);
y(x) = 0
eqn:=solve(eval(subs(x=0,y(0)=K,ans)),{cos(lambda^(1/2))});
1/2 1/2 1/2
eqn := {cos(lambda ) = lambda sin(lambda )}
eval(ans,eqn);
/ 1/2 \
|sin(lambda x) 1/2 |
y(x) = |---------------- + cos(lambda x)| K
| 1/2 |
\ lambda /
[править: Если вас интересуют реальные значения лямбды, то вот еще кое-что.]
restart;
de := diff(diff(y(x),x),x) + lambda*y(x) = 0:
bcs := D(y)(0) = K, D(y)(1) = 0:
ans := dsolve({de,bcs}, y(x)):
ans := collect(ans, K);
/ / (1/2) \
|sin\lambda x/
ans := y(x) = |------------------
| (1/2)
\ lambda
/ (1/2)\ / (1/2) \\
cos\lambda / cos\lambda x/|
+ -----------------------------------| K
(1/2) / (1/2)\ |
lambda sin\lambda / /
# The following equation must hold in order that your
# original boundary condition D(y)(0) = y(0) holds.
eqn := eval(subs(x=0, y(0)=K,ans));
/ (1/2)\
K cos\lambda /
eqn := K = ----------------------------
(1/2) / (1/2)\
lambda sin\lambda /
spec := [solve(eqn)];
[
[
[
spec := [{K = 0, lambda = lambda},
[
/ 2\ ]
| / (1/2) \ | ]
< | / 2\ | >]
|K = K, lambda = RootOf\tan(_Z) \_Z / - 1/ | ]
\ / ]
all_spec := map(allvalues, spec):
# Select only those elements of `all_spec` which satisfy `eqn`.
# (One of the float RootOfs returned by `allvalues` doesn't
# satisfy `eqn` above.
all_spec := select(u->is(simplify(fnormal(evalf[20](eval((rhs-lhs)(eqn),u))),
zero)
= 0),
all_spec):
map(print, all_spec):
{K = 0, lambda = lambda}
/ 2\
| / (1/2) \ |
< | / 2\ | >
|K = K, lambda = RootOf\tan(_Z) \_Z / - 1, 0.8603335890/ |
\ /
/ 2\
| / (1/2) \ |
< | / 2\ | >
|K = K, lambda = RootOf\tan(_Z) \_Z / - 1, 3.425618459/ |
\ /
# These below are the mentioned solutions, using the above RootOf's
# having so-called "float descriptors", which means they can
# be further approximated to arbitrary precision using `evalf`.
p_sols := {seq([eval(ans, K=eval(K,all_spec[i])),
[lambda=eval(lambda,all_spec[i])]],
i=1..nops(all_spec))}:
#map(print, p_sols):
# For fun, now approximate using default precision.
fp_sols := evalf(p_sols):
seq(print(eval(fp_sols[i][1], fp_sols[i][2])), i=1..nops(fp_sols)):
y(x) = 0.
y(x) = (1.162339833 sin(0.8603335890 x)
+ 1.000000000 cos(0.8603335890 x)) K
y(x) = (0.2919180907 sin(3.425618459 x)
+ 1.000000002 cos(3.425618459 x)) K