Могут ли БД Graph работать с неуказанными конечными узлами?

Question

Я экспериментировал с neo4j для очень конкретного сценария, и мне не удалось заставить его работать хорошо - запросы возвращаются через несколько минут. Мне интересно, если это неправильная технология для работы?

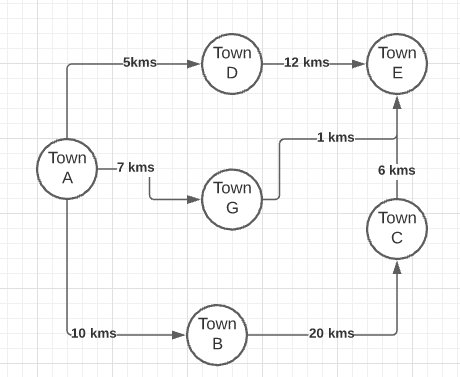
Ниже приведена упрощенная версия моего сценария. я имею Towns, которые связаны друг с другом маршрутами. У каждого маршрута есть расстояние.

Я пытаюсь задать вопрос: рассчитать кратчайший маршрут из Town A в любой другой город, доступный из Town A. В этом сценарии количество конечных узлов не указано. Для возврата этого запроса с небольшим набором данных требуется несколько минут, а для больших наборов данных с 50000 узлов он вообще не возвращается.

Если я задам вопрос: рассчитайте кратчайший маршрут из Town A к Town Eответ кажется мгновенным. В этом сценарии известны как начальный, так и конечный узлы.

Мой вопрос: подходят ли графические базы данных для открытых вопросов (рассчитайте кратчайший маршрут из Town A в любой другой город, доступный из Town A)? Если да, то неужели только мой подход к структурированию данных снижает производительность?

Answer 1

Ваша структура данных выглядит хорошо (возможно, вы могли бы добавить вершину "Пересечение" с ребром "ROAD" с длиной, сохраненной на ребре ROAD, но не знаете, какие данные у вас есть), и ДА, это определенно хороший вариант использования для графики.

Я нечасто использовал Neoj4, но проблема, скорее всего, заключается в подходе, который вы используете с задействованным алгоритмом (запросом).

Neo4j должен легко справиться с тем, чего вы хотите достичь. Я бы рекомендовал посмотреть несколько видеороликов Neo4j по этой теме и подражать их подходу к алгоритмам кратчайшего пути.

Neo4j(кратчайший путь): https://youtu.be/baEeRfuK1Nk

База данных графов, которую я всегда использовал для их реализации, всегда была на TigerGraph, но все базы данных графов могли бы быстро обрабатывать 50000 узлов.

TigerGraph (кратчайший путь): https://youtu.be/Ra0qORVKsWs

EDITED (добавление ссылок на документацию):

NEO4J

Алгоритм кратчайшего пути от одного источника

Документы: https://neo4j.com/docs/graph-algorithms/current/labs-algorithms/single-source-shortest-path/

ТИГЕРГРАФ

Кратчайший путь от одного источника (невзвешенный)

Документы: https://docs.tigergraph.com/v/2.6/graph-algorithm-library#single-source-shortest-path-unweighted

Код: https://github.com/tigergraph/gsql-graph-algorithms/blob/master/algorithms/schema-free/shortest_ss_no_wt.gsql

Кратчайший путь от одного источника (взвешенный)

Документы: https://docs.tigergraph.com/v/2.6/graph-algorithm-library#single-source-shortest-path-weighted

Код: https://github.com/tigergraph/gsql-graph-algorithms/blob/master/algorithms/schema-free/shortest_ss_any_wt.gsql

Answer 2

Поскольку существуют другие базы данных графов и другие языки запросов графов, вот как решить проблему с помощью Objectivity / DB и его языка запросов DO . (См. Следующий вопрос о схеме и настройке графа: Ссылка на схему и настройку. )

      CREATE WEIGHT CALCULATOR routeDistance {
    minimum:   0,
    default:   0, 
    edges: {
          ()-[r:Road]->(): r.distance
    }
};

Match m = MAX WEIGHT 100.0 routeDistance 
            ((:Town {name == 'TownA'})-[*]->(tEnd:Town)) 
            group by tEnd.name 
            order by Weight(m) asc 
            return tEnd.name, weight(m);

Запрос начинается с указания МАКСИМАЛЬНОГО ВЕСА, который служит для ограничения поиска. Установите для этого значения значение, превышающее максимальный вес, который будет встречаться, если вы хотите просмотреть все возможные результаты. Затем мы используем определяемый пользователем калькулятор веса «routeDistance», чтобы указать, как должны быть вычислены веса ребер (см. Связанный вопрос для описания этого). Затем мы группируем по конечной точке (tEnd.name) и упорядочиваем по вес для каждой конечной точки.

Результаты, основанные на указанном графике:

      {
  _Projection
  {
    tEnd.name:'TownD',
    weight(m):3.00000
  },
  _Projection
  {
    tEnd.name:'TownB',
    weight(m):4.00000
  },
  _Projection
  {
    tEnd.name:'TownE',
    weight(m):4.00000
  },
  _Projection
  {
    tEnd.name:'TownF',
    weight(m):8.00000
  },
  _Projection
  {
    tEnd.name:'TownG',
    weight(m):11.0000
  },
  _Projection
  {
    tEnd.name:'TownH',
    weight(m):21.0000
  },
  _Projection
  {
    tEnd.name:'TownC',
    weight(m):31.0000
  }
}