функция uniroot() в исходном коде не работает с модификацией; Не удалось выяснить ошибку
Я пытался узнать координаты пересечения двух кривых в R. Входные данные - это координаты эмпирических точек из двух кривых. Мое решение - использовать функцию curve_intersect(). Мне нужно сделать это для 2000 повторений (т.е. 2000 пар кривых). Итак, я поместил данные в два списка. Каждый список содержит 1000 фреймов данных с координатами x и y одной кривой в каждом фрейме данных.
Вот мои данные: данные
Ниже приведен код, который я использовал.
threshold_or1 <- map2_df(recall_or1_4, precision_or1_4,
~curve_intersect(.x, .y, empirical = TRUE, domain = NULL))
# recall_or_4 is a list of 2000 data frames. Each data frame
# |contains coordinates from curve #1.
# precision_or_4 is a list of 2000 data frames. Each data frame
# |contains coordinates from curve #2.
Я получил это сообщение об ошибке ниже.
Error in uniroot(function(x) curve1_f(x) - curve2_f(x), c(min(curve1$x), : f() values at end points not of opposite sign
Так как функция curve_intersect() может быть успешно применена к некоторым отдельным фреймам данных из двух списков. Я запустил следующий код, чтобы точно увидеть, какая пара фреймов данных привела к сбою процесса.
test <- for (i in 1:2000){
curve_intersect(recall_or1_4[[i]], precision_or1_4[[i]], empirical = TRUE, domain = NULL)
print(paste("i=",i))}
Затем я получил следующее сообщение, которое означает, что процесс выполняется успешно, пока не достигнет пары данных #460. Итак, я проверил эту индивидуальную пару данных.
[1] "i= 457"
[1] "i= 458"
[1] "i= 459"
Error in uniroot(function(x) curve1_f(x) - curve2_f(x), c(min(curve1$x), : f() values at end points not of opposite sign
Я построил пары данных #460.
test1 <- precision_or1_4[[460]] %>% mutate(statistics = 'precision')
test2 <- recall_or1_4[[460]] %>% mutate(statistics = 'recall')
test3 <- rbind(test1, test2)
test3 <- test3 %>% mutate(statistics = as.factor(statistics))
curve_test3 <- ggplot(test3, aes(x = x, y = y))+
geom_line(aes(colour = statistics))
curve_test3
Найдите координаты точки пересечения
Затем я изменил исходный код curve_intersect(). Исходный исходный код
curve_intersect <- function(curve1, curve2, empirical=TRUE, domain=NULL) {
if (!empirical & missing(domain)) {
stop("'domain' must be provided with non-empirical curves")
}
if (!empirical & (length(domain) != 2 | !is.numeric(domain))) {
stop("'domain' must be a two-value numeric vector, like c(0, 10)")
}
if (empirical) {
# Approximate the functional form of both curves
curve1_f <- approxfun(curve1$x, curve1$y, rule = 2)
curve2_f <- approxfun(curve2$x, curve2$y, rule = 2)
# Calculate the intersection of curve 1 and curve 2 along the x-axis
point_x <- uniroot(function(x) curve1_f(x) - curve2_f(x),
c(min(curve1$x), max(curve1$x)))$root
# Find where point_x is in curve 2
point_y <- curve2_f(point_x)
} else {
# Calculate the intersection of curve 1 and curve 2 along the x-axis
# within the given domain
point_x <- uniroot(function(x) curve1(x) - curve2(x), domain)$root
# Find where point_x is in curve 2
point_y <- curve2(point_x)
}
return(list(x = point_x, y = point_y))
}
Я изменил
uniroot()часть третьего оператора if. Вместо того, чтобы использовать
c(min(curve1$x), max(curve1$x)) в качестве аргумента
uniroot(), Я использовал
lower = -100000000, upper = 100000000. Модифицированная функция
curve_intersect_tq <- function(curve1, curve2, empirical=TRUE, domain=NULL) {
if (!empirical & missing(domain)) {
stop("'domain' must be provided with non-empirical curves")
}
if (!empirical & (length(domain) != 2 | !is.numeric(domain))) {
stop("'domain' must be a two-value numeric vector, like c(0, 10)")
}
if (empirical) {
# Approximate the functional form of both curves
curve1_f <- approxfun(curve1$x, curve1$y, rule = 2)
curve2_f <- approxfun(curve2$x, curve2$y, rule = 2)
# Calculate the intersection of curve 1 and curve 2 along the x-axis
point_x <- uniroot(function(x) curve1_f(x) - curve2_f(x),
lower = -100000000, upper = 100000000)$root
# Find where point_x is in curve 2
point_y <- curve2_f(point_x)
} else {
# Calculate the intersection of curve 1 and curve 2 along the x-axis
# within the given domain
point_x <- uniroot(function(x) curve1(x) - curve2(x), domain)$root
# Find where point_x is in curve 2
point_y <- curve2(point_x)
}
return(list(x = point_x, y = point_y))
}
Я попытался изменить значения
lower =, upper =аргументы. Это не работает. Я получил такое же сообщение об ошибке, как показано ниже.
curve_intersect_tq(recall_or1_4[[460]], precision_or1_4[[460]], empirical = TRUE, domain = NULL)
Error in uniroot(function(x) curve1_f(x) - curve2_f(x), c(min(curve1$x), :
f() values at end points not of opposite sign
Я также пробовал использовать
possibly(fun, NA)из пакета tidyverse в надежде, что процесс может работать даже с сообщением об ошибке. Не получилось, когда я использовал
(1)
possibly(curve_intersect(), NA) или (2)
possibly(uniroot(), NA)
Появилось такое же сообщение об ошибке.
Почему у меня появляется сообщение об ошибке? Какие могут быть возможные решения? Заранее спасибо.
1 ответ
Возможно, вы немного опоздаете на вечеринку, но вот почему ваш код все еще не работает и что вы можете сделать, в зависимости от того, что вы хотите получить из своего анализа:
Прежде всего, причина того, что ваш код не работает даже после адаптации, заключается в том, что вы просто говорите
uniroot искать в более широком окне
x. Однако лежащие в основе кривые никогда не пересекаются - просто нет никаких
curve1_f(x) - curve2_f(x) == 0 быть найденным.
Из документа
uniroot:
"Значения функции в конечных точках должны иметь противоположные знаки (или ноль), для extendInt="no"- значение по умолчанию".
В оригинале
curve_intersect реализация,
uniroot выполняет поиск в интервале x, который определен в ваших данных (это
c(min(curve1$x), max(curve1$x))). В вашем изменении вы говорите ему искать в интервале x
[-100000000, 100000000]. Вы могли бы также установить
extendInt = "yes", но это ничего не изменит.
Проблема не в интервале поиска, а в
approxfun!
approxfunпросто помогает вам путем интерполяции эмпирических данных между точками. Вне данных, которые вы передаете, возвращенная функция не будет знать, что делать.
approxfun позволяет указать явные значения для
y который должен быть возвращен за пределами эмпирически определенного окна (с его параметрами
yleft/
yright) или позволяет установить
ruleс каждой стороны.
В коде, который вы разместили выше,
rule = 2решает, что "используется значение на ближайшем экстремуме данных". Так,
approxfunне экстраполирует переданные вами данные. Он только расширяет известные.
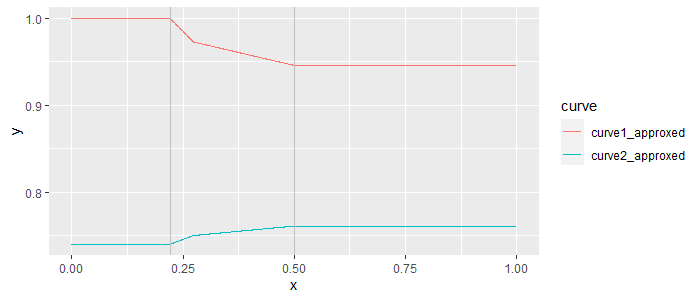
Мы можем представить, как
curve1_f и
curve2_f будет распространяться за пределы эмпирически определенного x-интервала в бесконечность:
tibble(
x = seq(0, 1, by = 0.001),
curve1_approxed = curve1_f(x),
curve2_approxed = curve2_f(x)
) %>%
pivot_longer(starts_with("curve"), names_to = "curve", values_to = "y") %>%
ggplot(aes(x = x, y = y, color = curve)) +
geom_line() +
geom_vline(xintercept = c(min(curve1$x), max(curve1$x)), color = "grey75")
Итак, теперь о том, что вы можете сделать, чтобы ваш код не падал:
(спойлер: это в значительной степени зависит от того, что вы пытаетесь достичь с помощью своего проекта)
- согласитесь, что в наблюдаемых пределах ваших данных нет пересечения.
Если вы не хотите делать никаких предположений, я бы посоветовал вам обернуть отображаемую функцию вtryCatchзаявление и позвольте ему потерпеть неудачу там, где готовое решение не дает никаких результатов. Давайте запустим это для той части вашего списка, которая раньше приводила к сбою всей системы:
threshold_or1.fix1 <- map2_df(
recall_or1_4, precision_or1_4,
~tryCatch({
curve_intersect(.x, .y, empirical = TRUE, domain = NULL)
}, error = function(e){
return(tibble(.rows = 1))
}),
.id = "i"
)
Теперь есть просто строка NA, когда
curve_intersect не может дать вам результат.
threshold_or1.fix1[459:461,]
# A tibble: 3 x 3
i x y
<chr> <dbl> <dbl>
1 459 0.116 0.809
2 460 NA NA
3 461 0.264 0.773
- попробуйте экстраполировать ваши данные с помощью линейной модели.
В этом случае мы будем использовать настраиваемуюcurve_intersect-функция. Обернем проблемноеunirootпозвонить вtryCatchи если корень не может быть найден, мы подберемlmдля каждой кривой и пустьunirootнайти пересечение на подобранных линейных линиях.
Это может иметь или не иметь смысла в свете вашего эксперимента, поэтому я позволю вам быть здесь судьей. И, очевидно, вы можете использовать другие модели, кроме упрощенных.lmесли ваши данные более сложные, чем это...
Просто чтобы визуализировать этот подход по сравнению со значением по умолчанию:
tibble(
x = seq(-1, 2, by = 0.001),
curve1_approxed = curve1_f(x),
curve2_approxed = curve2_f(x),
curve1_lm = predict(lm(y ~ x, data = curve1), newdata = tibble(x = x)),
curve2_lm = predict(lm(y ~ x, data = curve2), newdata = tibble(x = x))
) %>%
pivot_longer(starts_with("curve"), names_to = "curve", values_to = "y") %>%
ggplot(aes(x = x, y = y, color = curve)) +
geom_line() +
geom_vline(xintercept = c(min(curve1$x), max(curve1$x)), color = "grey75")
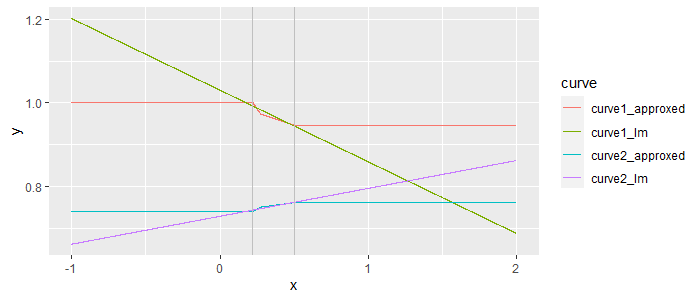
Вы видите, где
approxfun "терпит неудачу", с
lm мы делаем это предположение, что мы можем экстраполировать линейно и найти пересечение вокруг
x = 1.27 за пределами вашего наблюдаемого кадра.
Чтобы пойти на второй подход и включить экстраполяцию с
lmв нашем поиске вы могли бы собрать что-то вроде этого:
(здесь тоже только третий
if редактируется.)
curve_intersect_custom <- function(curve1, curve2, empirical=TRUE, domain=NULL) {
if (!empirical & missing(domain)) {
stop("'domain' must be provided with non-empirical curves")
}
if (!empirical & (length(domain) != 2 | !is.numeric(domain))) {
stop("'domain' must be a two-value numeric vector, like c(0, 10)")
}
if (empirical) {
return(
tryCatch({
# Approximate the functional form of both curves
curve1_f <- approxfun(curve1$x, curve1$y, rule = 2)
curve2_f <- approxfun(curve2$x, curve2$y, rule = 2)
# Calculate the intersection of curve 1 and curve 2 along the x-axis
point_x <- uniroot(
f = function(x) curve1_f(x) - curve2_f(x),
interval = c(min(curve1$x), max(curve1$x))
)$root
# Find where point_x is in curve 2
point_y <- curve2_f(point_x)
return(list(x = point_x, y = point_y, method = "approxfun"))
}, error = function(e) {
tryCatch({
curve1_lm_f <- function(x) predict(lm(y ~ x, data = curve1), newdata = tibble(x = x))
curve2_lm_f <- function(x) predict(lm(y ~ x, data = curve2), newdata = tibble(x = x))
point_x <- uniroot(
f = function(x) curve1_lm_f(x) - curve2_lm_f(x),
interval = c(min(curve1$x), max(curve1$x)),
extendInt = "yes"
)$root
point_y <- curve2_lm_f(point_x)
return(list(x = point_x, y = point_y, method = "lm"))
}, error = function(e) {
return(list(x = NA_real_, y = NA_real_, method = NA_character_))
})
})
)
} else {
# Calculate the intersection of curve 1 and curve 2 along the x-axis
# within the given domain
point_x <- uniroot(function(x) curve1(x) - curve2(x), domain)$root
# Find where point_x is in curve 2
point_y <- curve2(point_x)
}
return(list(x = point_x, y = point_y))
}
Для проблемных элементов списка теперь пытается экстраполировать наивно подогнанный
lm модель:
threshold_or1.fix2 <- map2_df(
recall_or1_4, precision_or1_4,
~curve_intersect_custom(.x, .y, empirical = TRUE, domain = NULL),
.id = "i"
)
threshold_or1.fix2[459:461,]
# A tibble: 3 x 4
i x y method
<chr> <dbl> <dbl> <chr>
1 459 0.116 0.809 approxfun
2 460 1.27 0.813 lm
3 461 0.264 0.773 approxfun
Надеюсь, это немного поможет в понимании и решении вашей проблемы:)