Сглаживание пути робота
Я рассчитываю кратчайший путь робота на плоскости с полигональными препятствиями. Все работает хорошо и быстро, проблем нет. Но как сгладить путь, чтобы он стал пышным? Ниже приведено изображение пути, соединяющего вершины с прямой линией. PS Робот это просто круг.
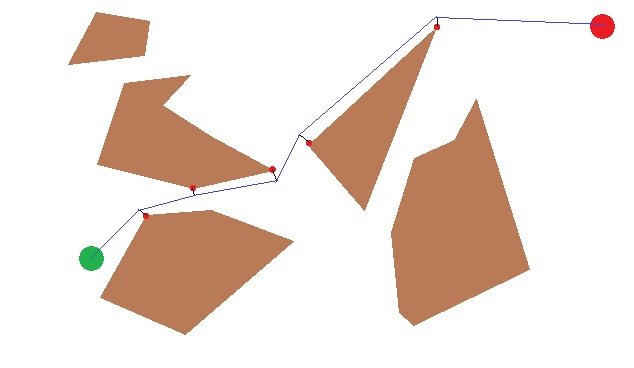
4 ответа
Эта статья может быть полезной. Похоже, это нетривиальная проблема. Аннотация:
Автоматические средства построения графиков должны вычислять пути между вершинами простого многоугольника, которые помимо того, чтобы оставаться внутри, должны демонстрировать определенные эстетические свойства. Некоторые из них требуют включения некоторой информации о многоугольной форме, не слишком далеко от фактического кратчайшего пути. Мы представляем алгоритм для вычисления локально выпуклой области, которая "содержит" кратчайший евклидовый путь среди двух вершин простого многоугольника. Область имеет граничную форму, которая "следует" за формой кратчайшего пути. Кубический сплайн Безье во внутренней области обеспечивает "короткую и гладкую" кривую без столкновений между двумя заданными вершинами. Полученные результаты представляются эстетически приятными, а используемые методы могут представлять самостоятельный интерес. Они элементарны и осуществимы. Рисунок 7 - это пример вывода, созданного нашей текущей реализацией.
Я много играл с техникой расчета траектории, когда пытался создавать реалистичные последовательности полетов, которые будут отображаться в Терагене. Сначала я попробовал использовать кривые Безье.
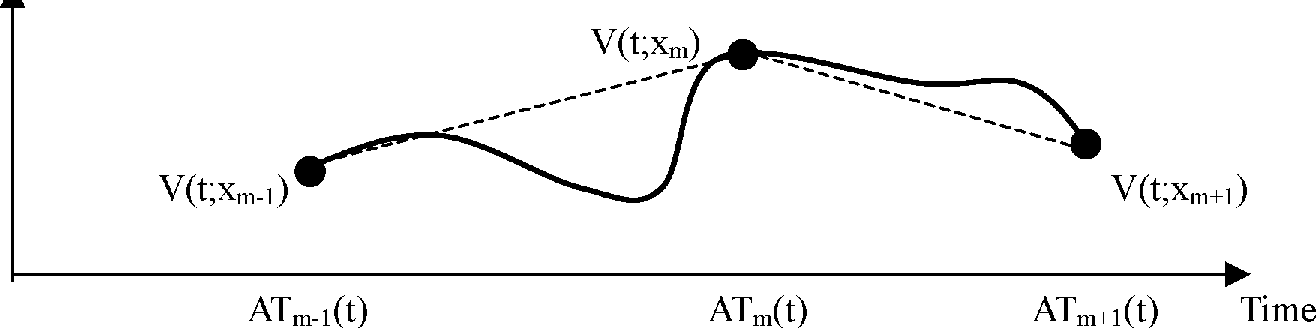
Но обнаружил, что (по крайней мере, для полетов) они не так полезны. Причина в том, что кривизна между кривыми является прерывистой, и поэтому ее нельзя использовать для расчета непрерывного правильного угла крена для пролета. Также трудно быть уверенным, что кривая не пересекает гору.
Я отвлекся. То, как я в конце концов остановился, было простым путем, основанным на массе, и превратило его в покорность.
Разделите путь на множество маленьких сегментов, чем больше, тем лучше. Для каждой точки немного переместите ее в направлении, чтобы уменьшить угол между ней и ее соседями и от препятствий. Повторите много раз, пока путь не успокоится.
k = 0.01 // Adjust the values of k and j to your liking.
j = 0.01 // Small values take longer to settle. Larger values are unstable.
For each point P
normal_vector = vector_to_previous_point + vector_to_next_point
obstacle_vector = vector_to_nearest_obstacle
obstacle_distance = magnitude(obstacle_vector)
obstacle_vector *= obstacle_distance^2
P += (normal_vector * k) - (obstacle_vector * j)
Преимущество такого рода методов релаксации конечных элементов заключается в том, что вы можете запрограммировать в нем все виды ограничений, и путь будет зависеть от некоторого компромисса между ними, в зависимости от весов (в данном случае j и k).
Если вы увлекаетесь робототехникой, почему бы не присоединиться к предложению по робототехнике?
Разве вы не можете просто сделать путь извилистым при фактическом выполнении алгоритма следования по пути? Если вы оставите путь как есть (т. Е. Соединены прямыми линиями), внедрив расстояние просмотра вперед ~1 метра (это значение будет зависеть от скорости вашего робота и количества заполненного пространства конфигурации, чтобы избежать препятствий) в Алгоритм управления, который вычисляет скорость каждого колеса, автоматически сгладит траекторию без предварительной обработки.
Вот быстрые изображения того, что я имею в виду... красная пунктирная линия - это путь, который фактически выполняется роботом, когда вы управляете точкой, основанной на расстоянии взгляда вперед. Расстояние прогнозирования просто вычисляет точку дальше вниз по траектории на произвольное расстояние.
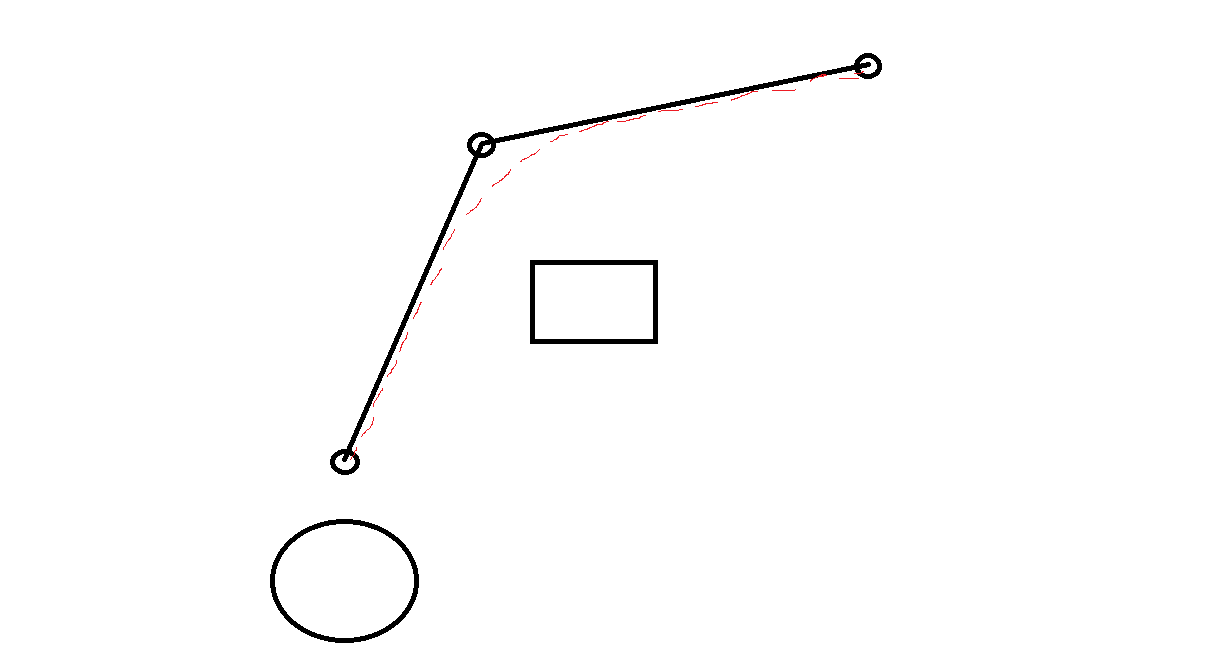
Опять же, единственное, о чем вам нужно беспокоиться, это сколько вы прокладываете препятствий, чтобы избежать их ударов. Обычно я считаю, что площадь препятствия дополняется половиной радиуса робота, но если вы управляете дистанцией опережения, вам, возможно, придется сделать это немного больше.
В случае с роботом мы не можем знать будущее. Мы должны нарисовать каждую точку, зная только местоположение робота и препятствия. Обычный метод создания изогнутых траекторий минимальной длины - моделировать робота с помощью круга и перемещать круг таким образом, чтобы он оставался в контакте с препятствиями. Просто держите один радиус, и повороты будут кривыми.
Если вам нужны кривые, а НЕ минимальное расстояние, попробуйте сделать вышеуказанный радиус пропорциональным расстоянию, на котором вы находитесь от вершины многоугольника.
Идея кривых Безье работает только для того, чтобы изогнуть путь назад. Это меняет место, где был робот. Обычно у роботов смена прошлого называется "изменой". Один из способов избежать изменения уже пройденного пути - смотреть в будущее. Но может ли робот видеть за углом? Вы должны уточнить правила лучше.