Как оптимизировать код умножения матриц (matmul) для быстрой работы на одном ядре процессора
Я работаю над концепциями параллельного программирования и пытаюсь оптимизировать пример умножения матриц на одном ядре. Самая быстрая реализация, которую я придумал, заключается в следующем:
/* This routine performs a dgemm operation
* C := C + A * B
* where A, B, and C are lda-by-lda matrices stored in column-major format.
* On exit, A and B maintain their input values. */
void square_dgemm (int n, double* A, double* B, double* C)
{
/* For each row i of A */
for (int i = 0; i < n; ++i)
/* For each column j of B */
for (int j = 0; j < n; ++j)
{
/* Compute C(i,j) */
double cij = C[i+j*n];
for( int k = 0; k < n; k++ )
cij += A[i+k*n] * B[k+j*n];
C[i+j*n] = cij;
}
}
Результаты как ниже. как уменьшить петли и увеличить производительность
login4.stampede(72)$ tail -f job-naive.stdout
Size: 480 Mflop/s: 1818.89 Percentage: 18.95
Size: 511 Mflop/s: 2291.73 Percentage: 23.87
Size: 512 Mflop/s: 937.061 Percentage: 9.76
Size: 639 Mflop/s: 293.434 Percentage: 3.06
Size: 640 Mflop/s: 270.238 Percentage: 2.81
Size: 767 Mflop/s: 240.209 Percentage: 2.50
Size: 768 Mflop/s: 242.118 Percentage: 2.52
Size: 769 Mflop/s: 240.173 Percentage: 2.50
Average percentage of Peak = 22.0802
Grade = 33.1204
2 ответа
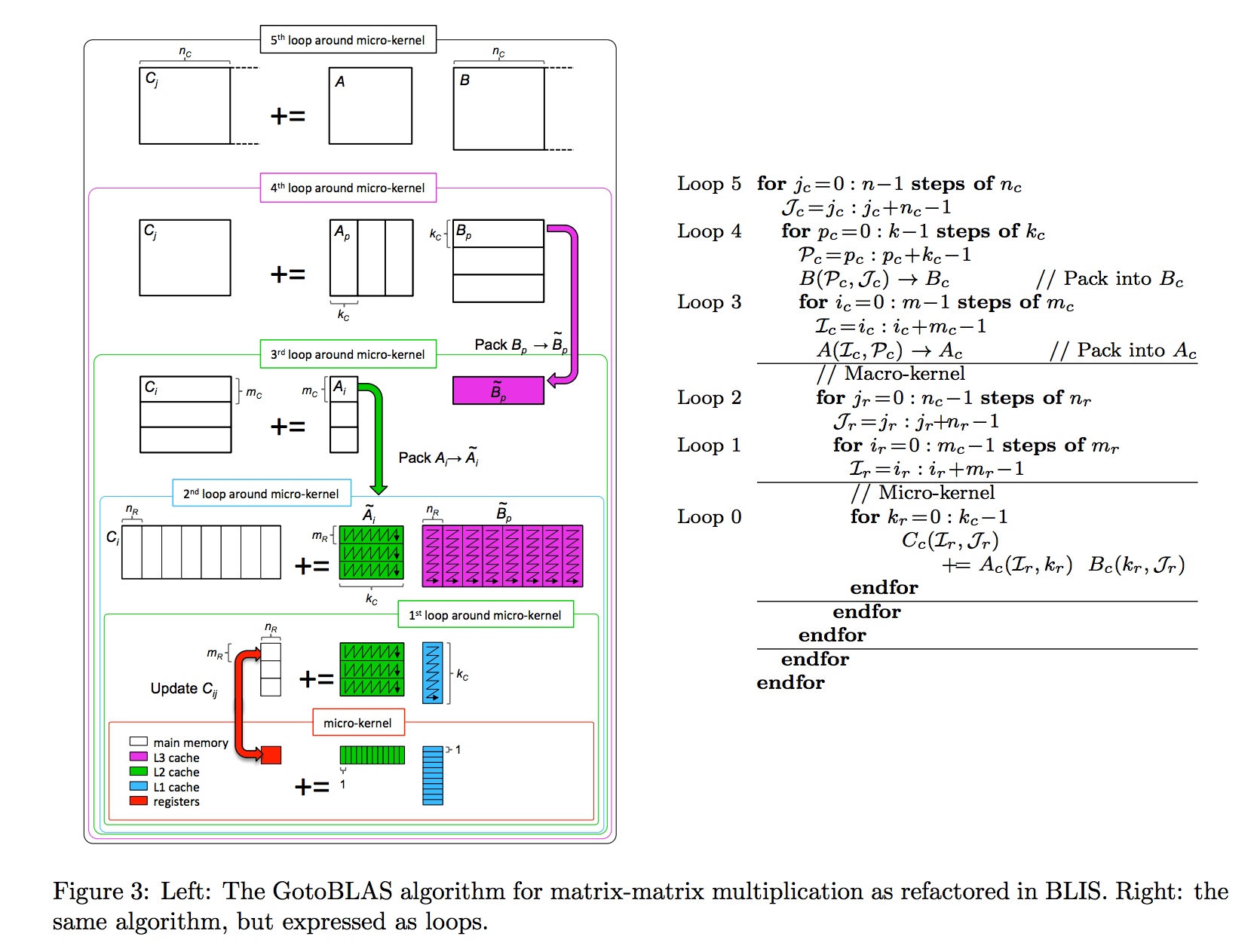
Современная реализация умножения матриц на процессорах использует алгоритм GotoBLAS. В основном циклы организованы в следующем порядке:
Loop5 for jc = 0 to N-1 in steps of NC
Loop4 for kc = 0 to K-1 in steps of KC
//Pack KCxNC block of B
Loop3 for ic = 0 to M-1 in steps of MC
//Pack MCxKC block of A
//--------------------Macro Kernel------------
Loop2 for jr = 0 to NC-1 in steps of NR
Loop1 for ir = 0 to MC-1 in steps of MR
//--------------------Micro Kernel------------
Loop0 for k = 0 to KC-1 in steps of 1
//update MRxNR block of C matrix
Ключевым моментом, лежащим в основе современных высокопроизводительных реализаций умножения матриц, является организация вычислений путем разбиения операндов на блоки для временной локализации (3 самых внешних цикла) и упаковка (копирование) таких блоков в смежные буферы, которые вписываются в различные уровни память для пространственной локализации (3 внутренних петли).
Приведенный выше рисунок (первоначально из этой статьи, непосредственно используемый в этом руководстве) иллюстрирует алгоритм GotoBLAS, реализованный в BLIS. Параметры блокировки кэша {MC, NC, KC} определяют размеры подматриц Bp (KC × NC) и Ai (MC × KC), так что они помещаются в различные кэши. Во время вычислений панели строк Bp непрерывно упаковываются в буфер Bp для размещения в кэше L3. Блоки Ai аналогичным образом упаковываются в буфер Ai для размещения в кэше L2. Размеры блоков регистров {MR, NR} относятся к подматрицам в регистрах, которые вносят вклад в C. В микроядре (самом внутреннем цикле) небольшая микро-плитка MR × NR C обновляется парой MR × KC и KC × NR осколки Ai и Bp.
Для алгоритма Штрассена со сложностью O(N^2.87) вам может быть интересно прочитать эту статью. Другие алгоритмы быстрого матричного умножения с асимптотической сложностью меньше, чем O(N^3), могут быть легко расширены в этой статье.
Следующие руководства могут быть полезны, если вы хотите узнать больше о том, как оптимизировать матричное умножение на процессорах:
[Как оптимизировать GEMM Wiki] ( https://github.com/flame/how-to-optimize-gemm/wiki)
[GEMM: от чистого C до оптимизированных для SSE микроядер] ( http://apfel.mathematik.uni-ulm.de/~lehn/sghpc/gemm/)
[BLISlab: песочница для оптимизации GEMM для процессора и ARM] ( https://github.com/flame/blislab)
Самый последний документ о том, как шаг за шагом оптимизировать GEMM на процессорах (с AVX2/FMA), можно скачать здесь: https://github.com/ULAFF/LAFF-On-HPC/blob/master/LAFF-On-PfHP.pdf
Курс MOOC (LAFF-On Программирование для высокой производительности): https://github.com/ULAFF/LAFF-On-HPC
Мой C я довольно ржавый, и я не знаю, что из следующего оптимизатор уже делает, но здесь идет...
Поскольку практически все время тратится на создание точечного продукта, позвольте мне просто оптимизировать это; Вы можете построить оттуда.
double* pa = &A[i];
double* pb = &B[j*n];
double* pc = &C[i+j*n];
for( int k = 0; k < n; k++ )
{
*pc += *pa++ * *pb;
pb += n;
}
Ваш код, вероятно, тратит больше времени на арифметику индекса, чем что-либо еще. Мой код использует +=8 а также +=(n<<3), что намного эффективнее. (Примечание: double принимает 8 байт.)
Другие оптимизации:
Если вы знаете ценность nВы можете "развернуть" хотя бы самый внутренний цикл. Это исключает накладные расходы for,
Даже если бы ты только знал, что n было четным, вы могли повторяться n/2 раза, удваивая код на каждой итерации. Это бы сократило for накладные расходы в два раза (прибл.)
Я не проверял, можно ли лучше сделать умножение матрицы в мажорной строке или в мажорной колонке. +=8 быстрее чем +=(n<<3); это было бы небольшое улучшение во внешних петлях.
Другой способ "развернуть" - сделать два точечных произведения в одном и том же внутреннем цикле. (Полагаю, я слишком сложен, чтобы даже объяснить.)
Процессоры "гиперскалярные" в наши дни. Это означает, что они могут, в некоторой степени, делать несколько вещей одновременно. Но это не значит, что вещи, которые должны выполняться последовательно, могут быть оптимизированы таким образом. Выполнение двух независимых точечных произведений в одном цикле может предоставить больше возможностей для гиперскалирования.
Есть много способов прямых улучшений. Базовая оптимизация - это то, что написал Рик Джеймс. Кроме того, вы можете переставить первую матрицу по строкам, а вторую по столбцам. Тогда в ваших циклах for() вы всегда будете делать ++ и никогда не будете делать +=n. Циклы, по которым вы переходите, гораздо медленнее по сравнению с ++.
Но большинство из этих оптимизаций остаются верными, потому что хороший компилятор сделает их за вас, когда вы используете флаги -O3 или -O4. Он развернет циклы, повторно использует регистры, выполнит логические операции вместо умножений и т. Д. Он даже изменит порядок ваших for i а также for j петли при необходимости.
Основная проблема с вашим кодом заключается в том, что когда у вас есть матрицы NxN, вы используете 3 цикла, заставляя вас делать O(N^3) операции. Это очень медленно. Я думаю, что современные алгоритмы делают только ~O(N^2.37) операции ( ссылка здесь). Для больших матриц (скажем, N = 5000) это чертовски сильная оптимизация. Вы можете легко реализовать алгоритм Штрассена, который даст вам ~N^2.87 улучшение или использование в комбинации с алгоритмом Карацубы, который может ускорить процесс даже для регулярных скалярных оптимизаций. Не реализовывайте ничего самостоятельно. Загрузите реализацию с открытым исходным кодом. Умножение матриц как огромная тема с большим количеством исследований и очень быстрыми алгоритмами. Использование 3-х циклов не считается допустимым способом эффективной работы. Удачи
Вместо оптимизации вы можете запутать код, чтобы он выглядел как оптимизированный.
Вот матричное умножение с одним нулевым телом for петля (!):
/* This routine performs a dgemm operation
* C := C + A * B
* where A, B, and C are lda-by-lda matrices stored in column-major format.
* On exit, A and B maintain their input values.
* This implementation uses a single for loop: it has been optimised for space,
* namely vertical space in the source file! */
void square_dgemm(int n, const double *A, const double *B, double *C) {
for (int i = 0, j = 0, k = -1;
++k < n || ++j < n + (k = 0) || ++i < n + (j = 0);
C[i+j*n] += A[i+k*n] * B[k+j*n]) {}
}