Правильная обработка денормальных поплавков в ISO-Prolog
Денормальные поплавки - это нечто особенное:
Что в стандарте ISO-Prolog сказано о том, как с ними обращаться?
Мне ясно, что повышение evaluation_error(underflow)Исключение всякий раз, когда возникают эти денормальные значения, является правильным способом борьбы с ними, но это влечет за собой дополнительные затраты - необходимо проверять каждое созданное число с плавающей точкой.
Но как насчет режимов работы "сбрасывать денормальные значения до нуля" (FTZ) и "рассматривать денормальные значения как нулевые" (DAZ), которые предлагают многие процессоры? Могут ли реализации Prolog использовать их, и если да, то как они это делают правильно?
Достаточно ли (1) документировать использование этих режимов работы, (2) гарантировать, что денормальные значения сбрасываются до нуля одного и того же знака (FTZ), и (3) гарантировать, что денормальные значения рассматриваются как ноль одного и того же знака (DAZ)? Помогите, пожалуйста!
3 ответа
Не пропускайте их. Тем не менее, короткий ответ из ISO/IEC 13211-1:1995 9.1.4.2 Функция результата с плавающей запятой:
Должно быть определено реализацией,
выбирает ли процессор раунд(x) или уменьшение количества переполнений, когда 0 <|х|< FminН.
Но сначала назовем их субнормальными. Устаревшее (по крайней мере, согласно LIA 1:2012) понятие денормальное был (в ретроспективе) не очень полезным, поскольку предполагал некоторые деструктивные, деструктивные свойства. И нет: они не такие уж особенные, как вы предлагаете. Чтобы убедиться в этом, рассмотрим числовую строку действительных чисел. Числа, которые могут быть представлены точно, отмечены и становятся все ближе и ближе друг к другу при приближении к нулю (с обеих сторон). Субнормальные - это те, которые наиболее близки к нулю. Расстояние между ними и нулем такое же, как расстояние между наименьшими нормальными числами. Это их аномалия (или, так сказать, денормальная). Если вы удалите сейчас эти субнормальные явления, вы получите гигантский разрыв, который вызовет еще больше числовых аномалий. Это как если бы вы соскребали на линейке отметки рядом с нулем, а затем использовали эту сломанную линейку для измерения1.. Таким образом, в отсутствие субнормальных значений остальные числа не являются нормальными, как можно было бы подумать, а скорее ненормальными, склонными к еще большему количеству ошибок.
Если вам не нравится читать Кахана по теме, которую я, тем не менее, предлагаю, могу я отослать вас к книге Густафсона " Конец ошибки", которая объясняет субнормальные явления гораздо лучше, чем я.
В 13211-1 есть возможность исключить субнормальные изменения, но это сделано только для совместимости с очень RISCy устаревшими архитектурами.
Вот и все формальное соответствие. В долгосрочной перспективе может оказаться многообещающим подход в стиле Unum, CLP(BNR) и Prolog IV.
1) То есть если вы округляете до нуля. Если вместо этого вы создаете значения исключений / продолжения, более точные числовые свойства будут сохраняться, пока такие исключения не возникают.
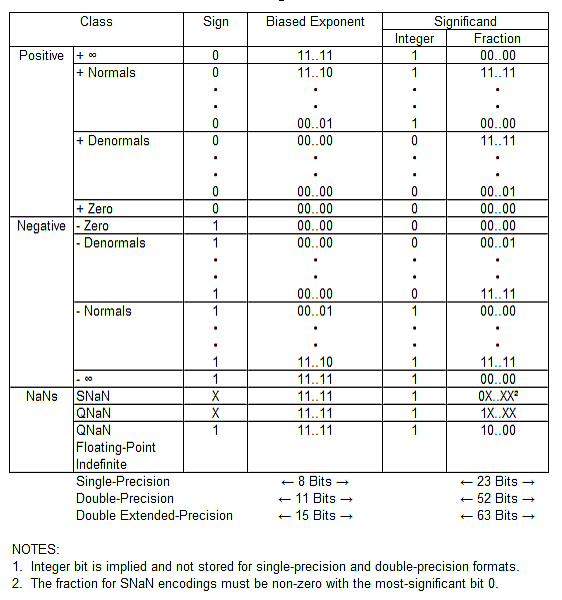
В разделе 7.1.3 стандарт ISO-Prolog определяет набор F как набор чисел, которые может представлять выбранный вами формат с плавающей запятой. Этот набор может включать или не включать денормализованные значения, разрешены оба варианта.
Когда результат вычисления (абсолютно) больше нуля и меньше наименьшего нормализованного значения, у вас есть выбор между
- округление до значения, представимого в F
- создание исключения потери значимости
Согласно разделу 9.1.4.2, этот выбор определяется реализацией, т.е. вы должны его задокументировать.
Это небольшой тестовый пример, чтобы увидеть, может ли ваша система Prolog возвращать субнормальные значения в результате арифметики (без сброса до нуля, ~FTZ):
/* SWI-Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308.
X = -5.0e-324.
/* Jekejeke Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308.
X = -4.9E-324
И это новое дополнение в API, которое не одинаково для систем Prolog, показывающее передачу аргументов субнормальных величин (нет денормальных равных нулю, ~DAZ):
/* SWI-Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308,
float_parts(X,M,B,E).
X = -5.0e-324,
M = -0.5,
B = 2,
E = -1073.
/* Jekejeke Prolog */
?- X is 2.2250738585072011e-308 - 2.2250738585072012e-308,
sys_float_mantissa(X,M), sys_float_exponent(X,E), sys_float_radix(X,R).
X = -4.9E-324,
M = -1,
E = -1074,
R = 2
Результат взят из MacBook Air 2019.