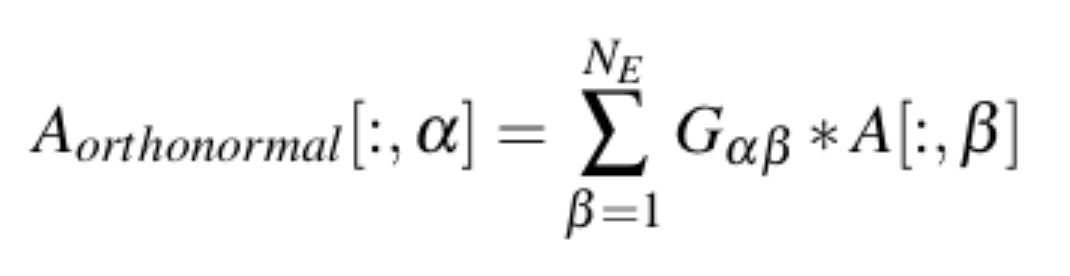Норма памяти - Cython
У меня есть функция, которой присваивается вектор обзора памяти, и я хочу вычислить норму этого вектора. До сих пор я добивался этого путем преобразования представления памяти в массив Numpy и вычисления нормы с помощью np.sqrt(V.dot(V)), Теперь я хочу избавиться от этого шага по соображениям скорости, но программа в какой-то момент завершается неудачно со следующей реализацией.
cdef do_something(np.double_t[::1] M_mem):
cdef:
int i
np.double_t norm_mv = 0
np.double_t norm_np = 0
np.ndarray[np.double_t, ndim=1] V = np.copy(np.asarray(M_mem))
# Original implementation -- working
norm_np = np.sqrt(V.dot(V))
# My failed try with memoryview -- not working
for i in range(M_mem.shape[0]):
norm_mv += M_mem[i]**2
norm_mv = np.sqrt(norm_mv)
# norm_mv != norm_np
Я подозреваю, что причиной этого является арифметика с плавающей точкой, которая мешает достаточно большим векторам. Существует ли численно устойчивый способ вычисления нормы просмотра памяти Cython?
ОБНОВИТЬ
После проверки выясняется, что ошибка округления, вероятно, не имеет смысла. Вместо этого происходит действительно странная вещь. Моя фактическая функция выглядит так:
@cython.boundscheck(False)
@cython.cdivision(True)
@cython.wraparound(False)
cdef np.double_t[:,::1] GS_coefficients(np.double_t[:,::1] M_mem):
cdef:
int n, i, k
int N_E = M_mem.shape[1]
np.ndarray[np.double_t, ndim=2] W = np.asarray(M_mem)
np.ndarray[np.double_t, ndim=2] V = np.copy(W)
np.double_t[:,::1] G = np.eye(N_E, dtype=np.float64)
np.longdouble_t norm = 0 # np.sqrt(V[:,0].dot(V[:,0]))
for i in range(M_mem.shape[0]):
norm += M_mem[i,0]**2
norm = sqrt(norm)
print("npx: ", np.sqrt(V[:,0].dot(V[:,0]))) # line 1
print("cp: ", norm) # line 2
V[:,0] /= norm
G[0,0] /= norm
for n in range(1, N_E):
for i in range(0, n):
G[n,i] = - (V[:,i].dot(W[:,n]))
V[:,n] += G[n,i] * V[:,i]
norm = np.sqrt(V[:,n].dot(V[:,n]))
V[:,n] /= norm
for i in range(n+1):
G[n,i] /= norm
return G
Я вставил print заявления, чтобы проверить, "насколько равны" результаты для norm мы. Странность в том, что теперь все работает нормально, как показано выше. Но когда я закомментирую первый оператор печати (строка 1), код нормально проходит через функцию, но вскоре завершается ошибкой в программе. То, что там происходит? Разве это не просто print утверждение, которое не должно даже повлиять на что-либо еще?
ОБНОВЛЕНИЕ 2
Вот моя попытка на минимальном, полном и проверяемом примере:
DEF N_E_cpt = 4
cimport cython
cimport numpy as np
import numpy as np
from libc.math cimport sqrt
@cython.boundscheck(False)
@cython.cdivision(True)
@cython.wraparound(False)
cdef np.double_t[:,::1] GS_coefficients(np.double_t[:,::1] M_mem):
"""Writes the coefficients, that the Gram-Schmidt procedure
provides in a Matrix and retruns it."""
cdef:
int n, i, k
int N_E = M_mem.shape[1]
np.ndarray[np.double_t, ndim=2] W = np.asarray(M_mem)
np.ndarray[np.double_t, ndim=2] V = np.copy(W)
np.double_t[:,::1] G = np.eye(N_E, dtype=np.float64)
np.longdouble_t norm = 0 # np.sqrt(V[:,0].dot(V[:,0]))
for i in range(M_mem.shape[0]):
norm += M_mem[i,0]**2
norm = sqrt(norm)
print("npx: ", np.sqrt(V[:,0].dot(V[:,0]))) # line 1
print("cp: ", norm) # line 2
V[:,0] /= norm
G[0,0] /= norm
for n in range(1, N_E):
for i in range(0, n):
G[n,i] = - (V[:,i].dot(W[:,n]))
V[:,n] += G[n,i] * V[:,i]
norm = np.sqrt(V[:,n].dot(V[:,n]))
V[:,n] /= norm
for i in range(n+1):
G[n,i] /= norm
return G
@cython.boundscheck(False)
@cython.cdivision(True)
@cython.wraparound(False)
cdef np.double_t[:,::1] G_mat(np.double_t[:,::1] M_mem):
"""Calls GS_coefficients and uses the coefficients to calculate
the entries of the transformation matrix G_ij"""
cdef:
np.double_t[:,::1] G_mem = GS_coefficients(M_mem)
int N_E = G_mem.shape[1]
np.double_t carr[N_E_cpt][N_E_cpt]
np.double_t[:,::1] G = carr
int n, i, j
# delete lower triangle in G
G[...] = G_mem
for i in range(N_E_cpt):
for j in range(0, i):
G[i,j] = 0.
for n in range(1, N_E):
for i in range(0, n):
for j in range(0, i+1):
G[n,j] += G_mem[n,i] * G[i,j]
return G
def run_test():
cdef:
np.double_t[:,::1] A_mem
np.double_t[:,::1] G
np.ndarray[np.double_t, ndim=2] A = np.random.rand(400**2, N)
int N = 4
A_mem = A
G = G_mat(A_mem)
X = np.zeros((400**2, N))
for i in range(0, N):
for j in range(0,i+1):
X[:,i] += G[i,j] * A[:,j]
print(X)
print("\n", X.T.dot(X))
run_test()
Я не думаю, что необходимо понимать, что делает этот код. Для меня загадка действительно, почему это print заявление имеет значение.
Поэтому этот код должен взять неортонормированный набор векторов, записанных как векторы столбцов в матрице A, и вернуть ортонормированную матрицу, которая ортонормирует набор векторов следующим образом:
Таким образом, A_{orthonormal} эквивалентен X-матрице в коде. Когда вы умножаете транспонирование ортонормированной матрицы на саму ортонормированную матрицу, вы получаете матрицу единства, то есть то, что вы получаете, пока print оператор # line1 находится там. Как только вы удалите его, вы также получите недиагональные записи, что означает, что матрица даже не ортогональна. Зачем?
1 ответ
Есть хотя бы опечатка
for i in range(M_mem.shape[0]):
norm += M_mem[i]**2
->
for i in range(M_mem.shape[0]):
norm_mv += M_mem[i]**2
Иначе, я рекомендую более идиоматическую версию ниже:
import numpy as np
cimport numpy as np
from libc.math cimport sqrt
def do_something(double[::1] M_mem):
cdef:
int i
double norm_mv = 0
double norm_np = 0
double[::1] V = np.copy(np.asarray(M_mem))
# Original implementation -- working
norm_np = np.sqrt(np.dot(V, V))
# My failed try with memoryview -- not working
for i in range(M_mem.shape[0]):
norm_mv += M_mem[i]**2
norm_mv = sqrt(norm_mv)
# norm_mv != norm_np
return norm_np, norm_mv
импортировать и импортировать NumPy и использовать скалярные математические функции из libc.math вместо версий NumPy. Вы все еще можете немного ускорить код, украсив подпрограмму @cython.boundscheck(False) (тебе нужно cimport cython затем).