Вычислить количество узлов по обе стороны от края дерева для заданных запросов.
Дано дерево с N узлами и N-1 ребром, и ребра удаляются в определенном порядке. После каждого удаления вам необходимо указать количество узлов, присутствующих в каждом из двух вновь созданных узлов.
Примечание: корень неизвестен; N<=300000; Например: дано дерево с 6 узлами, пронумерованными от 1 до 6, со следующими ребрами:
edge 1 >> 1 - 2
edge 2 >> 2 - 3
edge 3 >> 1 - 4
edge 4 >> 4 - 5
edge 5 >> 4 - 6
Теперь у нас есть перестановка от 1 до n-1 целых чисел, которая обозначает порядок, в котором> ребра будут удалены. Итак, предположим, что у нас есть перестановка: 4 3 1 2 5, Дерево:
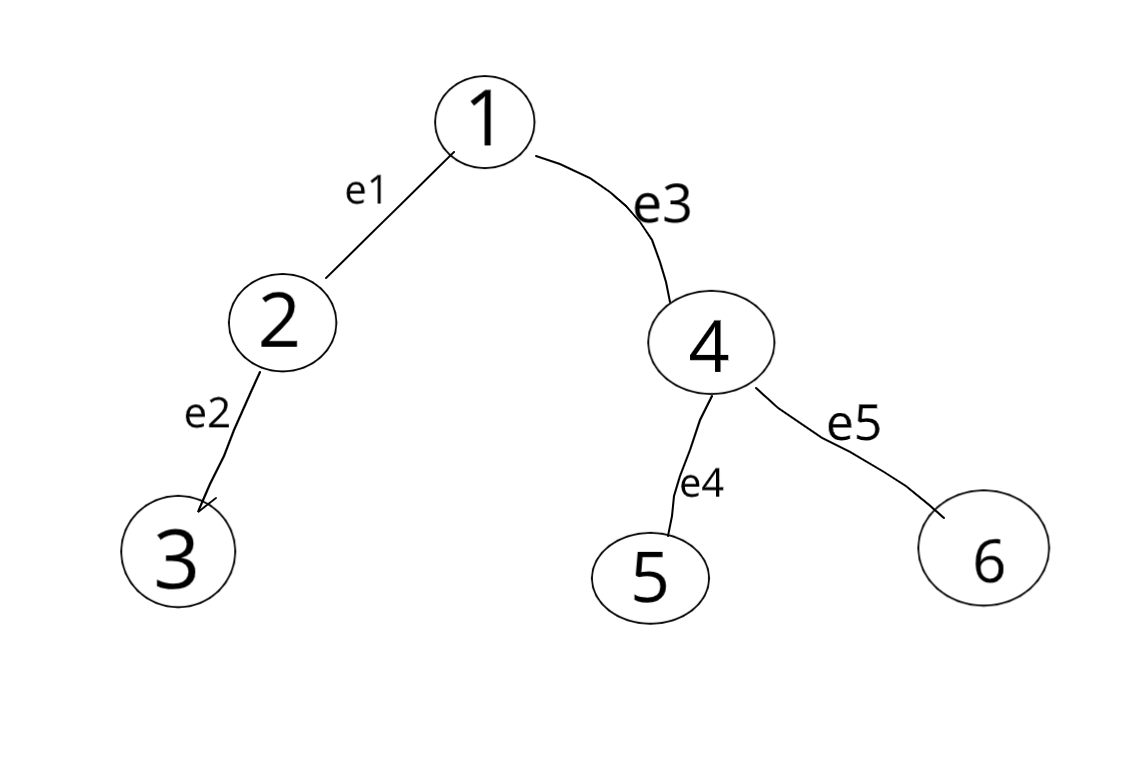
Результат будет в следующем виде:
Когда край 4 будет удален: ни один из узлов не будет разделен на: 1 и 5
Когда край 3 будет удален, количество узлов будет разделено на 2 и 3 (обратите внимание, что узел 5 уже удален)
Аналогично для более поздних краев вывод должен быть:
- Для кромки 1: 1 и 2
- Затем ребро 2: 1 и 1
- Затем край 5: 1 и 1
Мой подход заключается в том, что я создаю массив компонентов и выполняю BFS на одной стороне края в одном компоненте и обновляю компонент до нового значения и подсчитываю узлы. и если общее количество узлов в компоненте равно X, а count равно y, и выведите ans как y и Xy.
Это подход O(N2). Мне нужно лучшее решение, которое может дать мне ответ в N * log(N) .
любой другой подход, о котором может мне рассказать каждый. Это будет полезно.
Мой исходный код:
EdgeDeletion.class
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.DataInputStream;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;
public class EdgeDeletion {
public static void main(String[] args) throws IOException {
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
Reader s=new Reader();
int n = s.nextInt();
Edge[] edges = new Edge[n];
Graph G = new Graph(n);
for(int i = 1 ;i<n;i++)
{
int a =s.nextInt();
int b = s.nextInt();
G.addEdge(a, b);
edges[i] = new Edge(a, b);
}
int component[] = new int[n+1];
int sizeComp[] = new int[n+1];
Arrays.fill(component,1);
sizeComp[1] = n;
int D[] = new int[n];
for(int i = 1;i<n;i++)
{
D[i] = s.nextInt();
}
for(int i = 1 ;i<n;i++)
{
int a = edges[D[i]].a;
int b = edges[D[i]].b;
long ans = 0;
int c = component[a];
boolean[] v = new boolean[n+1];
v[b] = true;
Queue<Integer> queue = new LinkedList<>();
queue.add(a);
int size = 0;
while(!queue.isEmpty())
{
int k = queue.poll();
v[k] = true;
size++;
component[k] = i+1;
for(int no : G.adj[k])
{
if(!v[no]&&component[no]==c)
{
queue.add(no);
}
}
}
int size_prev = sizeComp[c];
sizeComp[c] = sizeComp[c] - size;
sizeComp[i+1] = size;
bw.write(Math.min(size,sizeComp[c])+" "+Math.Max(size,sizeComp[c])+\n");
}
bw.flush();
}
}
Graph.java
class Graph {
public int v;
public List<Integer> adj[];
public int degree[];
public Graph(int v) {
this.v = v;
adj = new ArrayList[v + 1];
degree = new int[v + 1];
for (int i = 1; i <= v; i++) {
adj[i] = new ArrayList<Integer>();
}
}
public void addEdge(int v, int w) {
adj[v].add(w);
adj[w].add(v);
degree[v]++;
degree[w]++;
}
public int findRootForMinHieght() {
Queue<Integer> que = new LinkedList<Integer>();
int x = v;
for (int i = 1; i <= this.v; i++) {
if (degree[i] == 1)
que.add(i);
}
while (x > 2) {
int t = que.poll();
x--;
for (int k : adj[t]) {
degree[k]--;
if (degree[k] == 1)
que.add(k);
}
}
while (que.size() > 1) {
que.poll();
}
return que.poll();
}
}
node.java
class node {
int parent;
int r;
HashSet<Integer> child;
public node(int parent) {
this.parent = parent;
child = new HashSet<>();
}
}
Edge.class
class Edge {
int a;
int b;
public Edge(int a, int b) {
this.a = a;
this.b = b;
}
}
Reader.java
class Reader {
final private int BUFFER_SIZE = 1 << 16;
private DataInputStream din;
private byte[] buffer;
private int bufferPointer, bytesRead;
public Reader() {
din = new DataInputStream(System.in);
buffer = new byte[BUFFER_SIZE];
bufferPointer = bytesRead = 0;
}
public Reader(String file_name) throws IOException {
din = new DataInputStream(new FileInputStream(file_name));
buffer = new byte[BUFFER_SIZE];
bufferPointer = bytesRead = 0;
}
public String readLine() throws IOException {
byte[] buf = new byte[64]; // line length
int cnt = 0, c;
while ((c = read()) != -1) {
if (c == '\n')
break;
buf[cnt++] = (byte) c;
}
return new String(buf, 0, cnt);
}
public int nextInt() throws IOException {
int ret = 0;
byte c = read();
while (c <= ' ')
c = read();
boolean neg = (c == '-');
if (neg)
c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
if (neg)
return -ret;
return ret;
}
public long nextLong() throws IOException {
long ret = 0;
byte c = read();
while (c <= ' ')
c = read();
boolean neg = (c == '-');
if (neg)
c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
if (neg)
return -ret;
return ret;
}
public double nextDouble() throws IOException {
double ret = 0, div = 1;
byte c = read();
while (c <= ' ')
c = read();
boolean neg = (c == '-');
if (neg)
c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
if (c == '.') {
while ((c = read()) >= '0' && c <= '9') {
ret += (c - '0') / (div *= 10);
}
}
if (neg)
return -ret;
return ret;
}
private void fillBuffer() throws IOException {
bytesRead = din.read(buffer, bufferPointer = 0, BUFFER_SIZE);
if (bytesRead == -1)
buffer[0] = -1;
}
private byte read() throws IOException {
if (bufferPointer == bytesRead)
fillBuffer();
return buffer[bufferPointer++];
}
public void close() throws IOException {
if (din == null)
return;
din.close();
}
}