Реализация алгоритма фильтрованной обратной проекции с использованием теоремы о центральном срезе в Matlab

Question

Я работаю над алгоритмом обратной проекции с фильтром, используя теорему о центральном срезе для домашнего задания, и, хотя я понимаю теорию на бумаге, я столкнулся с проблемой при ее реализации в Matlab. Мне предоставили скелет, которому я должен следовать, но есть шаг, который, как мне кажется, я неправильно понимаю. Вот что у меня есть:

function img = sampleFBP(sino,angs)

% This step is necessary so that frequency information is preserved: we pad
% the sinogram with zeros so that this is ensured.
sino = padarray(sino, floor(size(sino,1)/2), 'both');

% diagDim should be the length of an individual row of the sinogram - don't
% hardcode this!
diagDim = size(sino, 2);

% The 2DFT (2D Fourier transform) of our image will start as a matrix of
% all zeros.
fimg = zeros(diagDim);

% Design your 1-d ramp filter. 
rampFilter_1d  = abs(linspace(-1, 1, diagDim))';

rowIndex = 1;
for nn = angs
    % Each contribution to the image's 2DFT will also begin as all zero.
    imContrib = zeros(diagDim);

    % Get the current row of the sinogram - use rowIndex.
    curRow = sino(rowIndex,:);

    % Take the 1D Fourier transform the current row - be careful, as it's
    % necessary to perform ifftshift and fftshift as Matlab tends to
    % place zero-frequency components of a spectrum at the edges.
    fourierCurRow = fftshift(fft(ifftshift(curRow)));


    % Place the Fourier-transformed sino row and place it at the center of
    % the next image contribution. Add the ramp filter in Fourier domain.
    imContrib(floor(diagDim/2), :) = fourierCurRow;
    imContrib = imContrib * fft(rampFilter_1d);


    % Rotate the current image contribution to be at the correct angle on
    % the 2D Fourier-space image.
    imContrib = imrotate(imContrib, nn, 'crop');

    % Add the current image contribution to the running representation of
    % the image in Fourier space!
    fimg = fimg + imContrib;

    rowIndex = rowIndex + 1;
end

% Finally, just take the inverse 2D Fourier transform of the image! Don't
% forget - you may need an fftshift or ifftshift here.
rcon = fftshift(ifft2(ifftshift(fimg)));

Синограмма, которую я ввожу, - это просто результат радоновой функции фантома Шеппа-Логана от 0 до 179 градусов. Выполнение кода в его нынешнем виде дает мне черное изображение. Я думаю, что мне что-то не хватает в цикле, когда я добавляю FT строк к изображению. Исходя из моего понимания теоремы о центральном срезе, я думаю, что должно происходить следующее:

• Инициализируйте массив того же размера, что и 2DFT (например, diagDim x diagDim). Это пространство Фурье.

• Возьмите строку синограммы, которая соответствует информации линейного интеграла под одним углом, и примените к ней 1D FT.

• Согласно теореме о центральном срезе, FT этого линейного интеграла - это линия, проходящая через область Фурье, которая проходит через начало координат под углом, который соответствует углу, под которым была сделана проекция. Чтобы подражать этому, я беру FT этого линейного интеграла и помещаю его в центральную строку созданной мной матрицы diagDim x diagDim.

• Затем я беру FT созданного мною одномерного линейного фильтра и умножаю его на FT линейного интеграла. Умножение в области Фурье эквивалентно свертке в пространственной области, так что это сворачивает линейный интеграл с фильтром.

• Теперь я поворачиваю всю матрицу на угол, под которым была сделана проекция. Это должно дать мне матрицу diagDim x diagDim с единственной линией информации, проходящей через центр под углом. Matlab увеличивает размер матрицы при ее повороте, но поскольку синограмма была дополнена в начале, информация не теряется, и матрицы все еще могут быть добавлены

• Если все эти пустые матрицы с одной линией через центр сложить вместе, это должно дать мне полное 2D FT изображения. Все, что нужно сделать, это взять обратный 2D FT, и исходное изображение должно быть результатом.

Если проблема, с которой я столкнулся, носит концептуальный характер, я был бы признателен, если бы кто-нибудь мог указать, где я напортачил. Если вместо этого это вещь Matlab (я все еще новичок в Matlab), я был бы признателен за то, чтобы узнать, что я пропустил.

Answer 1

Код, который вы опубликовали, является довольно хорошим примером фильтрованной обратной проекции (FBP), и я считаю, что он может быть полезен людям, которые хотят изучить основы FBP. Можно использовать функциюiradon(...)в MATLAB (см. здесь) для выполнения FBP с использованием множества фильтров. В вашем случае, конечно, дело в том, чтобы изучить основы теоремы о центральном срезе, и поэтому поиск кратчайшего пути - не главное. Я также многому научился и освежил свои знания, отвечая на ваш вопрос!

Теперь ваш код отлично прокомментирован и описывает шаги, которые необходимо предпринять. Есть несколько тонких [программных] проблем, которые необходимо исправить, чтобы код работал нормально.

Во-первых, ваше представление изображения в области Фурье может иметь отсутствующий массив из-за floor(diagDim/2)в зависимости от размера синограммы. Я бы изменил это наround(diagDim/2) иметь полный набор данных в fimg. Имейте в виду, что это может привести к ошибке для определенных размеров синограмм, если с ними не обращаться правильно. Я бы посоветовал вам визуализироватьfimg чтобы понять, что это за отсутствующий массив и почему это важно.

Вторая проблема заключается в том, что синограмму необходимо транспонировать, чтобы она соответствовала вашему алгоритму. Следовательно, добавлениеsino = sino'. Опять же, я настоятельно рекомендую вам попробовать код без этого, чтобы увидеть, что произойдет! Обратите внимание, что вдоль представлений должно выполняться нулевое заполнение, чтобы избежать артефактов из-за наложения имен. В этом ответе я продемонстрирую это на примере.

В-третьих и самое главное, imContrib является временным держателем для массива вдоль fimg. Следовательно, он должен иметь тот же размер, что иfimg, так

imContrib = imContrib * fft(rampFilter_1d);

следует заменить на

imContrib(floor(diagDim/2), :) = imContrib(floor(diagDim/2), :)' .* rampFilter_1d;

Обратите внимание, что фильтр Ramp линейен в частотной области (спасибо @Cris Luengo за исправление этой ошибки). Поэтому вам следует отказаться отfft в fft(rampFilter_1d) поскольку этот фильтр применяется в частотной области (помните fft(x) разлагает область значений x, такую ​​как время, пространство и т. д., на ее частотное содержание).

Теперь полный пример, показывающий, как это работает с модифицированным фантомом Шеппа-Логана:

angs = 0:359; % angles of rotation 0, 1, 2... 359
init_img = phantom('Modified Shepp-Logan', 100); % Initial image 2D [100 x 100]
sino = radon(init_img, angs); % Create a sinogram using radon transform

% Here is your function ....

% This step is necessary so that frequency information is preserved: we pad
% the sinogram with zeros so that this is ensured.
sino = padarray(sino, floor(size(sino,1)/2), 'both');

% Rotate the sinogram 90-degree to be compatible with your codes definition of view and radial positions
% dim 1 -> view
% dim 2 -> Radial position
sino = sino'; 

% diagDim should be the length of an individual row of the sinogram - don't
% hardcode this!
diagDim = size(sino, 2);

% The 2DFT (2D Fourier transform) of our image will start as a matrix of
% all zeros.
fimg = zeros(diagDim);

% Design your 1-d ramp filter. 
rampFilter_1d  = abs(linspace(-1, 1, diagDim))';

rowIndex = 1;
for nn = angs

    % fprintf('rowIndex = %g => nn = %g\n', rowIndex, nn);
    % Each contribution to the image's 2DFT will also begin as all zero.
    imContrib = zeros(diagDim);

    % Get the current row of the sinogram - use rowIndex.
    curRow = sino(rowIndex,:);

    % Take the 1D Fourier transform the current row - be careful, as it's
    % necessary to perform ifftshift and fftshift as Matlab tends to
    % place zero-frequency components of a spectrum at the edges.
    fourierCurRow = fftshift(fft(ifftshift(curRow)));


    % Place the Fourier-transformed sino row and place it at the center of
    % the next image contribution. Add the ramp filter in Fourier domain.
    imContrib(round(diagDim/2), :) = fourierCurRow;
    imContrib(round(diagDim/2), :) = imContrib(round(diagDim/2), :)' .* rampFilter_1d; % <-- NOT fft(rampFilter_1d)


    % Rotate the current image contribution to be at the correct angle on
    % the 2D Fourier-space image.
    imContrib = imrotate(imContrib, nn, 'crop');

    % Add the current image contribution to the running representation of
    % the image in Fourier space!
    fimg = fimg + imContrib;

    rowIndex = rowIndex + 1;
end

% Finally, just take the inverse 2D Fourier transform of the image! Don't
% forget - you may need an fftshift or ifftshift here.
rcon = fftshift(ifft2(ifftshift(fimg)));

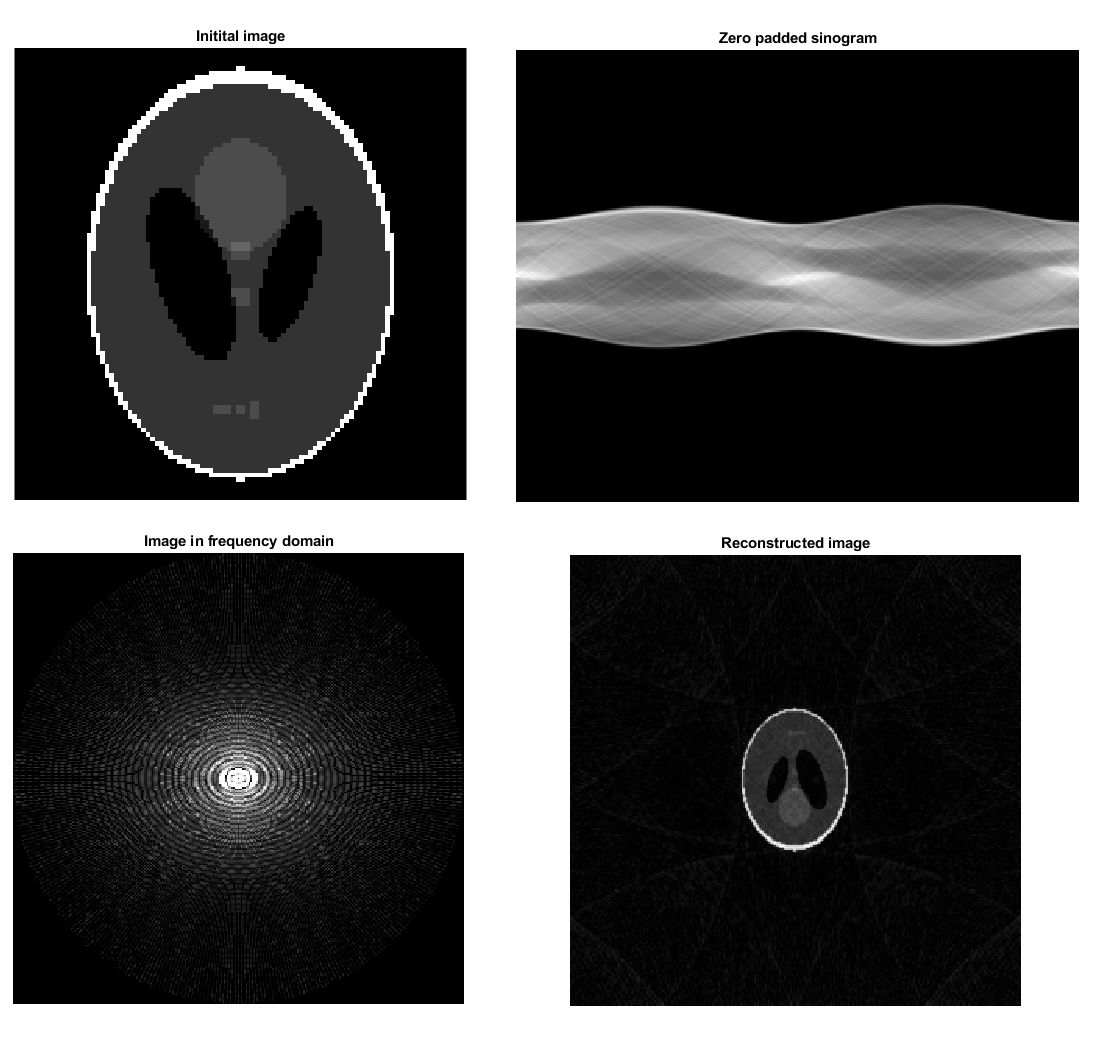
Обратите внимание, что ваше изображение имеет сложную ценность. Итак, я используюimshow(abs(rcon),[])чтобы показать изображение. Пара полезных изображений (пища для размышлений) с окончательно восстановленным изображениемrcon:

И вот то же изображение, если вы закомментируете шаг заполнения нуля (т.е. закомментируете sino = padarray(sino, floor(size(sino,1)/2), 'both');):

Обратите внимание на различный размер объектов на реконструированных изображениях с нулевым заполнением и без него. Объект сжимается, когда синограмма дополняется нулями, поскольку радиальное содержимое сжимается.