Найдите "центр" некоторых гистограмм с EMD в качестве метрики расстояния.

Question

Учитывая некоторые гистограммы с одинаковым количеством сегментов, мне нужно найти "центр" этих гистограмм. "Центр" - это гистограмма, так что сумма расстояний Земного движителя до нее от всех других гистограмм является минимальной.

Например, учитывая 4 гистограммы A, B, C, D, алгоритм должен вывести новую гистограмму X такой, что EMD(X, A) + EMD(X, B) + EMD(X, C) + EMD(X, D) это минимум.

Простое среднее арифметическое не может найти "центр", вот пример.

Мне нужно вычислить "центр" миллионов гистограмм, так как я могу эффективно найти "центр". Если быстрого алгоритма не существует, есть ли хороший пример?

=== редактировать ===

Добавлен пример, чтобы прояснить мою проблему.

Answer 1

Неформально дистанция движения землеройных машин рассматривает каждое распределение или в данном случае гистограмму как кучу грязи. Поиск центра в соответствии с EMD состоит в нахождении точки, которая минимизирует произведение каждой единицы площади гистограммы на расстояние, на которое она должна быть перемещена. Например, перемещение ячейки гистограммы с 7 элементами одна единица имеет такое же EMD, как перемещение ячейки гистограммы с 1 элементом 7 единиц. Я предполагаю, что ваше распределение имеет только одно измерение для простоты, но в противном случае эту центральную точку можно найти независимо по каждому измерению.

Расстояние до земного движителя на самом деле очень похоже на понятие в физике или статике; первый момент. Первый момент для формы определяется как произведение каждой единицы площади на расстояние этой единицы площади от центральной точки. Центральная точка находится так, что общая площадь по обе стороны от центральной точки (по любому главному измерению) одинакова.

Поклонники статики помнят, что эта центральная точка на самом деле является просто средним значением распределения площадей по каждому измерению. Определение EMD дает аналогичный результат. Таким образом, чтобы найти центроид EMD для вашей группы гистограмм, сделайте следующее:

Рассматривайте каждый элемент каждого бункера как единое целое. Присвойте каждой единице значение, связанное с этим бункером. Таким образом, если для данного измерения размер ячейки 0-10 имеет 5 записей, у вас будет 5 единиц каждая со значением 5 (среднее значение ячейки). Найдите среднее значение по всем единицам, и это будет ваше значение центроида для этого измерения. Повторите для всех измерений, если их больше одного, и все!

В этом тривиальном примере с 2 гистограммами, после обработки каждого элемента бина как одной единицы, медиана (и, следовательно, центр) равна 4. Очевидно, что перемещение центра выше или ниже 4 приведет к увеличению EMD на 5 и уменьшению его на 4..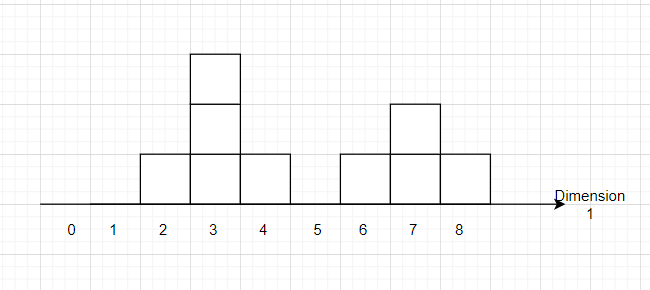

Если перейти к сути вашего вопроса, вы можете сделать немного лучше, чем сортировка всех элементов гистограммы, чтобы найти медиану, вместо использования QuickSelect для получения O(n) при средней временной сложности с O(nlogn) в худшем случае.

Answer 2

Если под "центром" вы ссылаетесь на медианное значение, это потребует сортировки набора данных; в этом случае гистограммы уже отсортированы. Понятно, что данные гистограмм, скорее всего, не будут представлены в виде списка; однако, поскольку альтернативы не указано, ответ будет структурирован как таковой.

сырые данные: список значений данные гистограммы: список кортежей "((мин, макс), количество)"

доступны необработанные данные:

#all data from histogram w/o bucket approximation
data = []
#sorting algorithm should be optimized for the size of the dateset 
#skip this step if data set sorted
data.sort()
median = (data[int(len(data)/2)]+data[round(len(data)/2)])/2

данные гистограммы:

#data from histogram only
data = []
#sort by min
#skip this step if histogram is already sorted
sort(key=lambda x:x[0][0])
#n is the data quantity
n = sum([bucket[1] for bucket in data])

#loop checks to see if median is captured in current bucket 
#by expanding the "net" by the current bucket size
rollingQuant = 0
median = None
for bucket in data:
    rollingQuant += bucket[1]
    #if median captured in bucket True
    if rollingQuant >= n/2:
        median = bucket[0]

выпуск:

• среднее значение с помощью только данных гистограммы невозможно вычислить; можно оценить; одним из примеров оценки может быть определение линейного уравнения с min max и количеством точек в корзине.