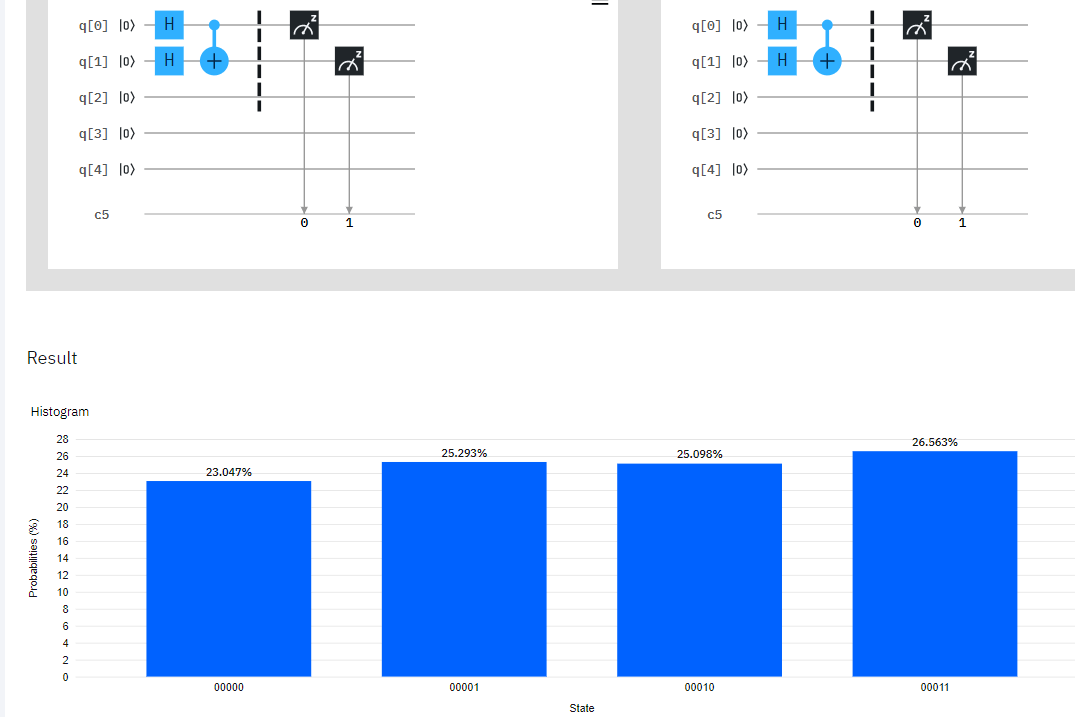
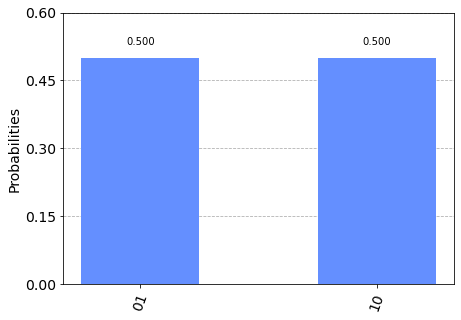
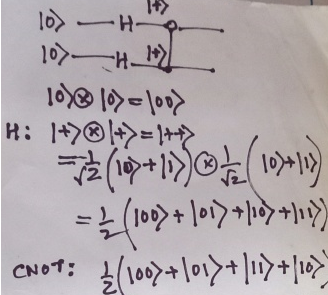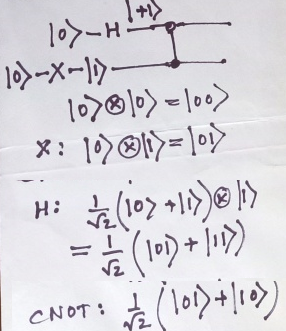2 запутанный кубит дает все состояния с 25%

Question

Мы запутываем два кварка; после измерения дает либо | 01>, либо | 10> с вероятностью 50%(независимо от их предыдущих состояний, они всегда дают противоположные состояния)

когда я запутываю 2 кубита с помощью Cnot, это дает | 00>, | 01>, | 10>, | 11> все с вероятностью 25%. Зачем???

Answer 1

Созданная вами схема действительно делает это: сначала применение вентилей Адамара к | 00> создаст состояние 1/2(|00>+|01>+|10>+|11>). Затем применение C-NOT приведет к | 01> к | 11> и | 11> к |01> (обычно | 10> к | 11> и | 11> к | 10> в соответствии с соглашением из учебника, но соглашение Qiskit делает его наоборот), поэтому ваше состояние на самом деле такое же, поэтому вы получаете вероятность 25% для каждого. Надеюсь, это достаточно ясно!

Answer 2

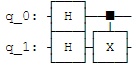
Давайте рассмотрим систему с двумя кубитами, в которой мы применяем оператор Адамара к обоим кубитам, а затем к CNOT (с первым кубитом в качестве управляющего бита).

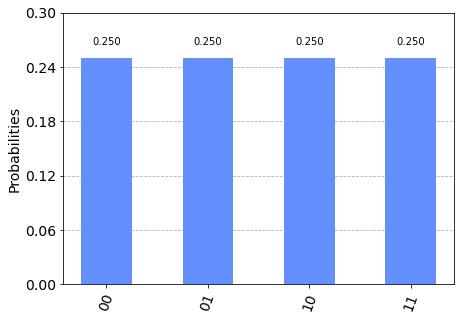
С помощью мы можем смоделировать вышеуказанную систему, как показано в приведенном ниже коде, и увидеть, что результаты соответствуют нашим ожиданиям (выходная система представляет собой равномерную суперпозицию 4 состояний с равной вероятностью).

      from qiskit import QuantumCircuit, Aer, execute
from qiskit.visualization import plot_histogram

qc = QuantumCircuit(2)
qc.h(0)  # |0> -> |+>
qc.h(1)  # |0> -> |+>
qc.cx(0,1)
qc.draw()

      backend = Aer.get_backend('statevector_simulator')
plot_histogram(execute(qc,backend).result().get_counts())

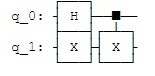
Чтобы получить желаемые состояния, нам нужно применить вентиль Адамара (H) к первому кубиту, вентиль НЕ (X) ко второму кубиту, а затем применить CNOT, чтобы получить желаемые запутанные состояния (состояние Белла):

Моделирование выше с qiskit:

      qc = QuantumCircuit(2)
qc.h(0)  # |0> -> |+>
qc.x(1)  # |0> -> |1>
qc.cx(0,1)
qc.draw()

      plot_histogram(execute(qc,backend).result().get_counts())