Создание двумерного гауссовского случайного поля из заданной двумерной дисперсии
Я пытался создать 2D-карту капель материи (гауссовское случайное поле), используя рассчитанную мной дисперсию. Эта дисперсия представляет собой двумерный массив. Я пробовал использовать numpy.random.normal, поскольку он позволяет вводить двухмерную дисперсию, но на самом деле не создает карту с тенденцией, которую я ожидаю от входных параметров. Одна из важных входных констант lambda_c должна проявляться как физический размер (диаметр) капли. Однако, когда я меняю свой lambda_c, размер капли не меняется, если вообще. Например, если я установил lambda_c = 40 парсеков, карте потребуются капли диаметром 40 парсеков. MWE для создания карты с использованием моей дисперсии:
import numpy as np
import random
import matplotlib.pyplot as plt
from matplotlib.pyplot import show, plot
import scipy.integrate as integrate
from scipy.interpolate import RectBivariateSpline
n = 300
c = 3e8
G = 6.67e-11
M_sun = 1.989e30
pc = 3.086e16 # parsec
Dds = 1097.07889283e6*pc
Ds = 1726.62069147e6*pc
Dd = 1259e6*pc
FOV_arcsec_original = 5.
FOV_arcmin = FOV_arcsec_original/60.
pix2rad = ((FOV_arcmin/60.)/float(n))*np.pi/180.
rad2pix = 1./pix2rad
x_pix = np.linspace(-FOV_arcsec_original/2/pix2rad/180.*np.pi/3600.,FOV_arcsec_original/2/pix2rad/180.*np.pi/3600.,n)
y_pix = np.linspace(-FOV_arcsec_original/2/pix2rad/180.*np.pi/3600.,FOV_arcsec_original/2/pix2rad/180.*np.pi/3600.,n)
X_pix,Y_pix = np.meshgrid(x_pix,y_pix)
conc = 10.
M = 1e13*M_sun
r_s = 18*1e3*pc
lambda_c = 40*pc ### The important parameter that doesn't seem to manifest itself in the map when changed
rho_s = M/((4*np.pi*r_s**3)*(np.log(1+conc) - (conc/(1+conc))))
sigma_crit = (c**2*Ds)/(4*np.pi*G*Dd*Dds)
k_s = rho_s*r_s/sigma_crit
theta_s = r_s/Dd
Renorm = (4*G/c**2)*(Dds/(Dd*Ds))
#### Here I just interpolate and zoom into my field of view to get better resolutions
A = np.sqrt(X_pix**2 + Y_pix**2)*pix2rad/theta_s
A_1 = A[100:200,0:100]
n_x = n_y = 100
FOV_arcsec_x = FOV_arcsec_original*(100./300)
FOV_arcmin_x = FOV_arcsec_x/60.
pix2rad_x = ((FOV_arcmin_x/60.)/float(n_x))*np.pi/180.
rad2pix_x = 1./pix2rad_x
FOV_arcsec_y = FOV_arcsec_original*(100./300)
FOV_arcmin_y = FOV_arcsec_y/60.
pix2rad_y = ((FOV_arcmin_y/60.)/float(n_y))*np.pi/180.
rad2pix_y = 1./pix2rad_y
x1 = np.linspace(-FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,n_x)
y1 = np.linspace(-FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,n_y)
X1,Y1 = np.meshgrid(x1,y1)
n_x_2 = 500
n_y_2 = 500
x2 = np.linspace(-FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,n_x_2)
y2 = np.linspace(-FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,n_y_2)
X2,Y2 = np.meshgrid(x2,y2)
interp_spline = RectBivariateSpline(y1,x1,A_1)
A_2 = interp_spline(y2,x2)
A_3 = A_2[50:450,0:400]
n_x_3 = n_y_3 = 400
FOV_arcsec_x = FOV_arcsec_original*(100./300)*400./500.
FOV_arcmin_x = FOV_arcsec_x/60.
pix2rad_x = ((FOV_arcmin_x/60.)/float(n_x_3))*np.pi/180.
rad2pix_x = 1./pix2rad_x
FOV_arcsec_y = FOV_arcsec_original*(100./300)*400./500.
FOV_arcmin_y = FOV_arcsec_y/60.
pix2rad_y = ((FOV_arcmin_y/60.)/float(n_y_3))*np.pi/180.
rad2pix_y = 1./pix2rad_y
x3 = np.linspace(-FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,n_x_3)
y3 = np.linspace(-FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,n_y_3)
X3,Y3 = np.meshgrid(x3,y3)
n_x_4 = 1000
n_y_4 = 1000
x4 = np.linspace(-FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,FOV_arcsec_x/2/pix2rad_x/180.*np.pi/3600.,n_x_4)
y4 = np.linspace(-FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,FOV_arcsec_y/2/pix2rad_y/180.*np.pi/3600.,n_y_4)
X4,Y4 = np.meshgrid(x4,y4)
interp_spline = RectBivariateSpline(y3,x3,A_3)
A_4 = interp_spline(y4,x4)
############### Function to calculate variance
variance = np.zeros((len(A_4),len(A_4)))
def variance_fluctuations(x):
for i in xrange(len(x)):
for j in xrange(len(x)):
if x[j][i] < 1.:
variance[j][i] = (k_s**2)*(lambda_c/r_s)*((np.pi/x[j][i]) - (1./(x[j][i]**2 -1)**3.)*(((6.*x[j][i]**4. - 17.*x[j][i]**2. + 26)/3.)+ (((2.*x[j][i]**6. - 7.*x[j][i]**4. + 8.*x[j][i]**2. - 8)*np.arccosh(1./x[j][i]))/(np.sqrt(1-x[j][i]**2.)))))
elif x[j][i] > 1.:
variance[j][i] = (k_s**2)*(lambda_c/r_s)*((np.pi/x[j][i]) - (1./(x[j][i]**2 -1)**3.)*(((6.*x[j][i]**4. - 17.*x[j][i]**2. + 26)/3.)+ (((2.*x[j][i]**6. - 7.*x[j][i]**4. + 8.*x[j][i]**2. - 8)*np.arccos(1./x[j][i]))/(np.sqrt(x[j][i]**2.-1)))))
variance_fluctuations(A_4)
#### Creating the map
mean = 0
delta_kappa = np.random.normal(0,variance,A_4.shape)
xfinal = np.linspace(-FOV_arcsec_x*np.pi/180./3600.*Dd/pc/2,FOV_arcsec_x*np.pi/180./3600.*Dd/pc/2,1000)
yfinal = np.linspace(-FOV_arcsec_x*np.pi/180./3600.*Dd/pc/2,FOV_arcsec_x*np.pi/180./3600.*Dd/pc/2,1000)
Xfinal, Yfinal = np.meshgrid(xfinal,yfinal)
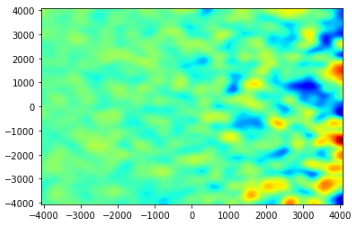
plt.contourf(Xfinal,Yfinal,delta_kappa,100)
plt.show()
Карта выглядит так: плотность капель увеличивается вправо. Однако размер капли не меняется, и карта выглядит практически одинаково, независимо от того, использую ли я lambda_c = 40*pc или lambda_c = 400 * pc.
Мне интересно, действительно ли функция np.random.normal не делает то, что я ожидаю? Мне кажется, что пиксельный масштаб карты и способ рисования образцов не связаны с размером капель. Возможно, есть лучший способ создать карту с использованием дисперсии, буду признателен за любое понимание.
Я ожидаю, что карта будет выглядеть примерно так: размеры капли меняются в зависимости от входных параметров для моей дисперсии: 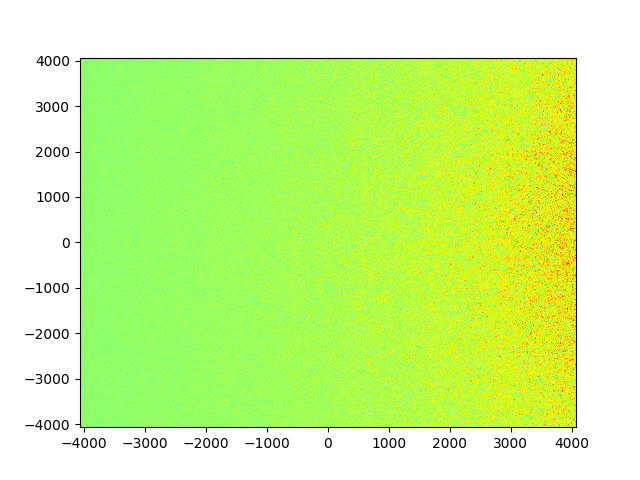
3 ответа
Совершенно другой и гораздо более быстрый способ - просто размыть массив delta_kappa с помощью гауссова фильтра. Попробуйте отрегулироватьsigma параметр для изменения размера капли.
from scipy.ndimage.filters import gaussian_filter
dk_gf = gaussian_filter(delta_kappa, sigma=20)
Xfinal, Yfinal = np.meshgrid(xfinal,yfinal)
plt.contourf(Xfinal,Yfinal,dk_ma,100, cmap='jet')
plt.show();
это изображение с sigma=20
это изображение с sigma=2.5
Это довольно популярная проблема (неожиданный сюрприз) астрономии и космологии.
Вы можете использовать lenstool: https://lenstools.readthedocs.io/en/latest/examples/gaussian_random_field.html
Вы также можете попробовать здесь:
https://andrewwalker.github.io/statefultransitions/post/gaussian-fields
Не говоря уж о:
https://github.com/bsciolla/gaussian-random-fields
Я не воспроизводю здесь код, потому что все заслуги вышеупомянутых авторов. Тем не менее, они все сразу вышли из поиска в Google: /
Проще всего, вероятно, использовать модуль Python FyeldGenerator, по-видимому, предназначенный именно для этой цели:
https://github.com/cphyc/FyeldGenerator
Итак (адаптировано из примера на github):
pip install FyeldGenerator
from FyeldGenerator import generate_field
from matplotlib import use
use('Agg')
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
# Helper that generates power-law power spectrum
def Pkgen(n):
def Pk(k):
return np.power(k, -n)
return Pk
# Draw samples from a normal distribution
def distrib(shape):
a = np.random.normal(loc=0, scale=1, size=shape)
b = np.random.normal(loc=0, scale=1, size=shape)
return a + 1j * b
shape = (512, 512)
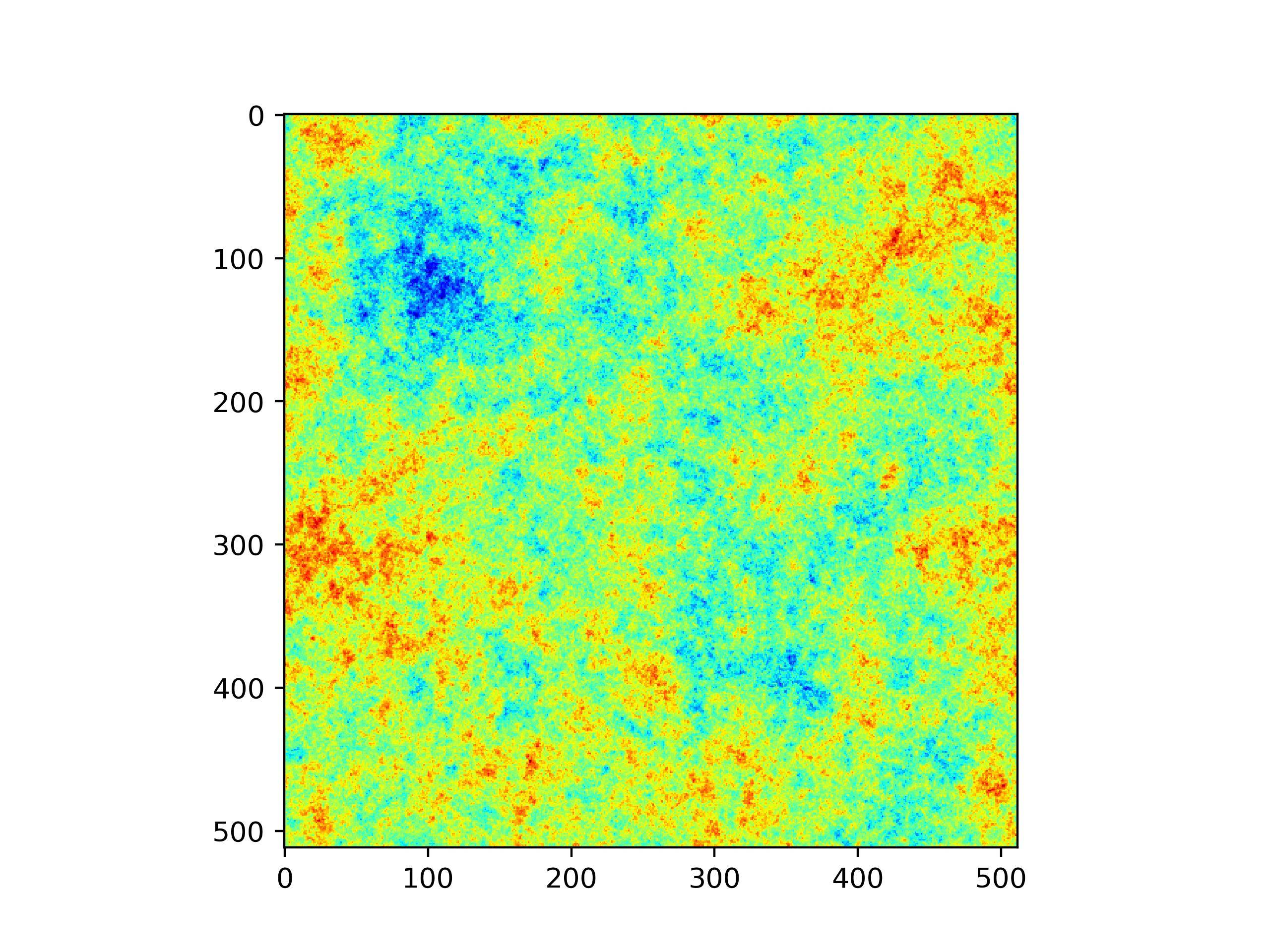
field = generate_field(distrib, Pkgen(2), shape)
plt.imshow(field, cmap='jet')
plt.savefig('field.png',dpi=400)
plt.close())
Это дает:
Для меня это выглядит довольно просто:)
PS: FoV подразумевает наблюдение гауссова случайного поля телескопом:)
ThunderFlash, попробуйте этот код, чтобы нарисовать карту:
# function to produce blobs:
from scipy.stats import multivariate_normal
def blob (positions, mean=(0,0), var=1):
cov = [[var,0],[0,var]]
return multivariate_normal(mean, cov).pdf(positions)
"""
now prepare for blobs generation.
note that I use less dense grid to pick blobs centers (regulated by `step`)
this makes blobs more pronounced and saves calculation time.
use this part instead of your code section below comment #### Creating the map
"""
delta_kappa = np.random.normal(0,variance,A_4.shape) # same
step = 10 #
dk2 = delta_kappa[::step,::step] # taking every 10th element
x2, y2 = xfinal[::step],yfinal[::step]
field = np.dstack((Xfinal,Yfinal))
print (field.shape, dk2.shape, x2.shape, y2.shape)
>> (1000, 1000, 2), (100, 100), (100,), (100,)
result = np.zeros(field.shape[:2])
for x in range (len(x2)):
for y in range (len(y2)):
res2 = blob(field, mean = (x2[x], y2[y]), var=10000)*dk2[x,y]
result += res2
# the cycle above took over 20 minutes on Ryzen 2700X. It could be accelerated by vectorization presumably.
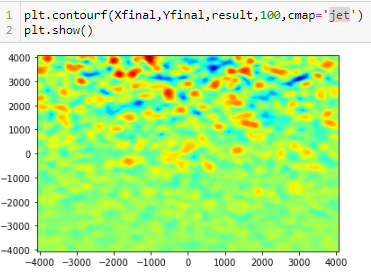
plt.contourf(Xfinal,Yfinal,result,100)
plt.show()
вы можете захотеть поиграть с var параметр в blob() для сглаживания изображения и с stepчтобы сделать его более сжатым. Вот изображение, которое я получил с помощью вашего кода (оси каким-то образом перевернуты и более плотные области вверху):