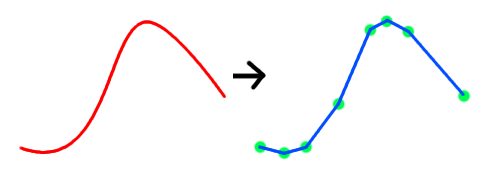
Алгоритм приведения одномерной функции к ломаной линии с небольшим количеством точек

Question

Проблема

Мой ввод - 1D функция y = f(x) и я хочу найти способ аппроксимировать эту функцию ломаной линией с небольшим количеством точек на некотором заданном интервале <x1, x2>:

Что пробовал:

Я решил эту проблему, построив ломаную линию с большим количеством точек (1000+), а затем уничтожив эту ломаную линию с помощью алгоритма Рамера – Дугласа – Пекера.

Итак, в (псевдо) питоне это будет примерно так:

def fn_to_low_poly(f, x1, x2):
    xs = numpy.linspace(x1, x2, 1000)
    ys = f(xs)
    return ramer_douglas_peucker_decimate(xs, ys, epsilon=0.001)

Это работает, но слишком сложно и медленно, и я уверен, что должен быть способ получше.

Я делаю это сейчас в python / numpy / scipy, но мне может потребоваться переписать его на C или Rust или что-то еще, поэтому меня не слишком заботит конкретный способ решения этой проблемы в python, я бы предпочел общий алгоритм, хотя буду благодарен за любую помощь.

Вопрос:

Есть ли алгоритм прямого уменьшения 1d функции (float -> float) в ломаную линию с небольшим количеством точек?