Генерация случайных мест в треугольной области

Question

Я хочу генерировать x а также y имеющий равномерное распределение и ограниченный [xmin,xmax] а также [ymin,ymax]

Точки (x,y) должны быть внутри треугольника.

Как я могу решить такую ​​проблему?

Answer 1

Вот некоторый код, который генерирует точки равномерно на произвольном треугольнике на плоскости.

import random

def point_on_triangle(pt1, pt2, pt3):
    """
    Random point on the triangle with vertices pt1, pt2 and pt3.
    """
    s, t = sorted([random.random(), random.random()])
    return (s * pt1[0] + (t-s)*pt2[0] + (1-t)*pt3[0],
            s * pt1[1] + (t-s)*pt2[1] + (1-t)*pt3[1])

Идея состоит в том, чтобы вычислить средневзвешенное значение трех вершин с весами, заданными случайным разрывом единичного интервала. [0, 1] на три части (равномерно по всем таким разрывам).

Вот пример использования, который генерирует 10000 точек в треугольнике:

pt1 = (1, 1)
pt2 = (2, 4)
pt3 = (5, 2)
points = [point_on_triangle(pt1, pt2, pt3) for _ in range(10000)]

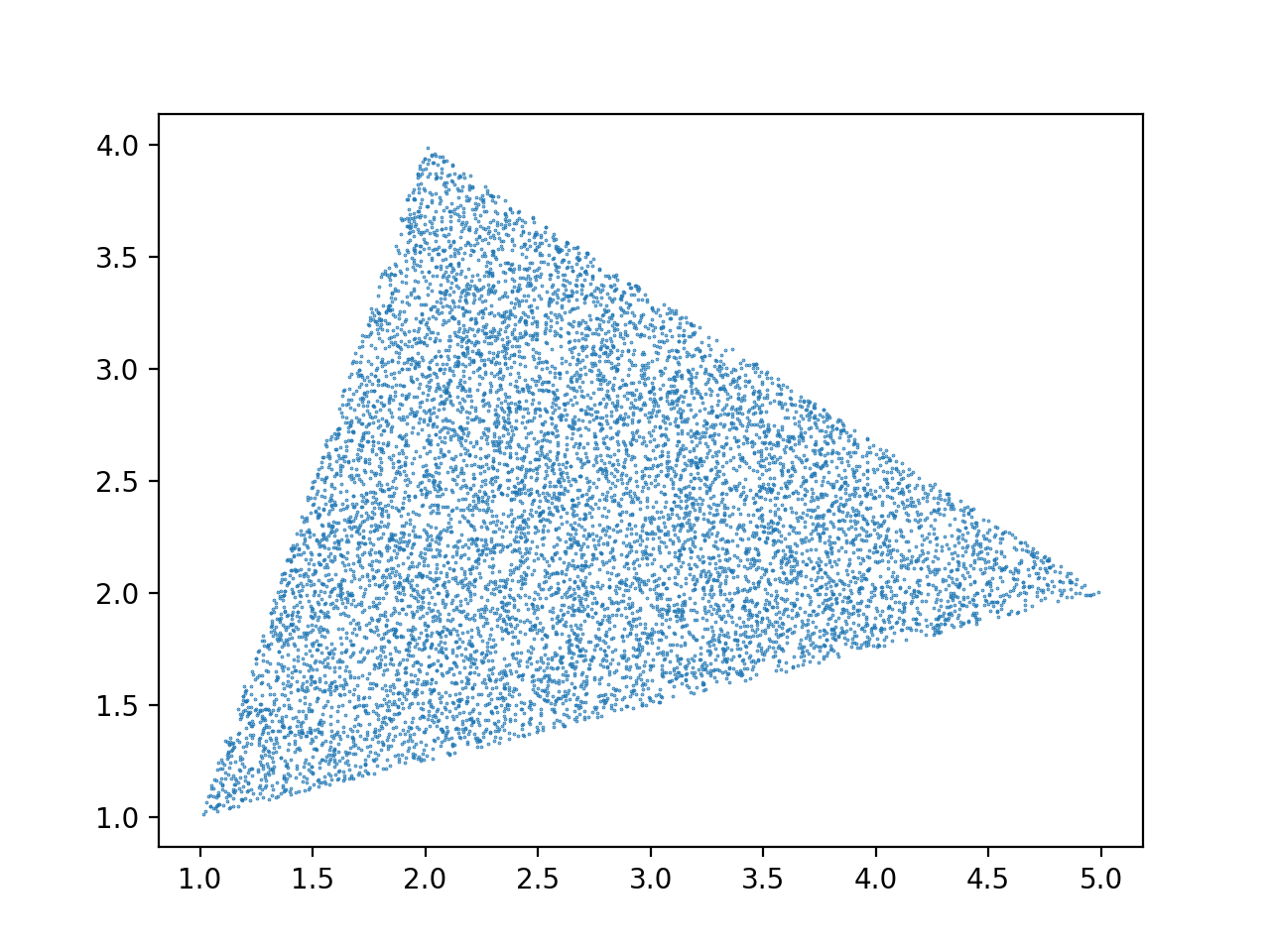
И сюжет, полученный из вышесказанного, демонстрирует однородность. Сюжет был сгенерирован этим кодом:

import matplotlib.pyplot as plt
x, y = zip(*points)
plt.scatter(x, y, s=0.1)
plt.show()

Вот изображение:

А так как вы пометили вопрос тегом "numpy", вот версия NumPy, которая генерирует несколько образцов одновременно. Обратите внимание, что он использует оператор умножения матриц @, представленный в Python 3.5 и поддерживаемый в NumPy >= 1.10. Вам нужно будет заменить это вызовом np.dot на старых версиях Python или NumPy.

import numpy as np

def points_on_triangle(v, n):
    """
    Give n random points uniformly on a triangle.

    The vertices of the triangle are given by the shape
    (2, 3) array *v*: one vertex per row.
    """
    x = np.sort(np.random.rand(2, n), axis=0)
    return np.column_stack([x[0], x[1]-x[0], 1.0-x[1]]) @ v


# Example usage
v = np.array([(1, 1), (2, 4), (5, 2)])
points = points_on_triangle(v, 10000)

Answer 2

Хорошо, пришло время добавить еще одну версию, я думаю. Известен алгоритм равномерной выборки в треугольнике, подробнее см. Статью 4.2.

Код Python:

import math
import random

import matplotlib.pyplot as plt

def trisample(A, B, C):
    """
    Given three vertices A, B, C, 
    sample point uniformly in the triangle
    """
    r1 = random.random()
    r2 = random.random()

    s1 = math.sqrt(r1)

    x = A[0] * (1.0 - s1) + B[0] * (1.0 - r2) * s1 + C[0] * r2 * s1
    y = A[1] * (1.0 - s1) + B[1] * (1.0 - r2) * s1 + C[1] * r2 * s1

    return (x, y)

random.seed(312345)
A = (1, 1)
B = (2, 4)
C = (5, 2)
points = [trisample(A, B, C) for _ in range(10000)]

xx, yy = zip(*points)
plt.scatter(xx, yy, s=0.2)
plt.show()

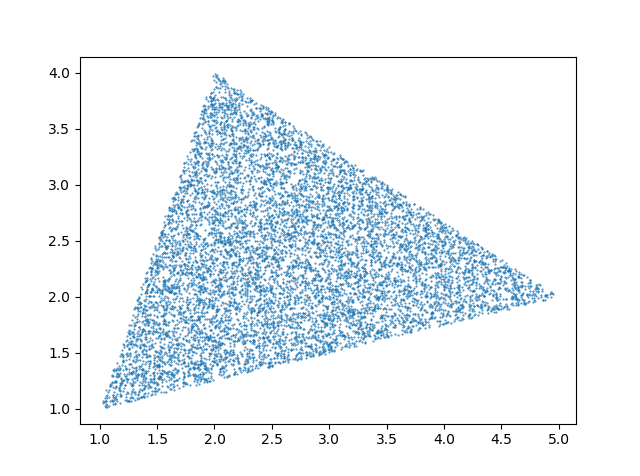
И результат выглядит так

Answer 3

Форма на треугольнике?

import numpy as np

N = 10 # number of points to create in one go

rvs = np.random.random((N, 2)) # uniform on the unit square
# Now use the fact that the unit square is tiled by the two triangles
# 0 <= y <= x <= 1 and 0 <= x < y <= 1
# which are mapped onto each other (except for the diagonal which has
# probability 0) by swapping x and y.
# We use this map to send all points of the square to the same of the
# two triangles. Because the map preserves areas this will yield 
# uniformly distributed points.
rvs = np.where(rvs[:, 0, None]>rvs[:, 1, None], rvs, rvs[:, ::-1])

Finally, transform the coordinates
xmin, ymin, xmax, ymax = -0.1, 1.1, 2.0, 3.3
rvs = np.array((ymin, xmin)) + rvs*(ymax-ymin, xmax-xmin)

Единые маргиналы? Простейшим решением было бы равномерно сконцентрировать массу на линии (ymin, xmin) - (ymax, xmax)

rvs = np.random.random((N,))
rvs = np.c_[ymin + (ymax-ymin)*rvs, xmin + (xmax-xmin)*rvs]

но это не очень интересно, не так ли?

Answer 4

Шаг (1): создать координату со случайным числом xr в [xmin, xmax] а также yr в [ymin, ymax] используя случайную функцию Python

Шаг (2): отменить координату и выбрать другую случайную, если [xr, yr] не лежит в треугольнике. Есть разные способы проверить, находится ли точка внутри выпуклого многоугольника, такого как треугольник, например:

• Разделение треугольника на три подреугольника и проверка того, имеет ли площадь трех подреугольников тот же размер, что и исходный треугольник
• Проверка для каждой линии треугольника, находится ли случайная координата на той же стороне плоскости, что и третья точка треугольника
• Использование барицентрических координат

Последние две стратегии объяснены более подробно в этой статье

Есть и другие методы, но эти три легко реализовать в Python даже с небольшим математическим образованием.

PS: Википедия также ссылается на эту статью, описывающую несколько методов с примерами кодов.