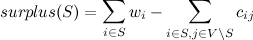Максимальное сокращение потока с перекрестными зависимостями

Question

У меня есть n заданий, которые выполняются с использованием старой системы. Если я изменю их на новую систему, я получу двойную выгоду за эту работу. Некоторые пары заданий (i, j) имеют зависимости. Смена работы, но не ее зависимая пара стоит xij. Задание 1 не может быть запущено в новой системе. Что такое идеальный набор рабочих мест, чтобы перейти на новую систему (за исключением, конечно, задания 1), чтобы максимизировать выгоду.

Это проблема алгоритма, перефразированная моими словами. Предполагается, что он должен быть уменьшен до некоторой формы максимального потока или циркуляции. У меня возникают чрезвычайные проблемы при разработке подхода из-за того, что затраты зависят от других заданий, переходящих на новую систему (кажется, я не могу связать статические значения с настройкой графа максимального потока и имею рабочее решение). Я думал об этом в течение некоторого времени и все еще изо всех сил пытаюсь найти достойный подход. Будем очень благодарны за любые предложения о том, как думать об атаке на эту проблему!

Answer 1

Давайте назначим b ₁ = −∞.

После того простого сокращения, которое вы описываете, в точности возникает проблема максимальной блокировки, например, определенная в "Алгоритме псевдопотока: новый алгоритм для задачи максимального потока", Hochbaum 2008:

Для заданного ориентированного графа G = (V, A) веса узлов положительные или отрицательные w _i для всех i ∈ V и веса неотрицательных дуг c _ij для всех (i,j) ∈ A. [...] Найдите a подмножество узлов S ⊆ V такое, что

является максимальным.

Они по-прежнему проводят связь между проблемой максимального разреза и проблемой минимального разреза. Для этого определим V '= V ∪ { s, t } и A' = A ∪ {(s, i) | w _i > 0 } ∪ {(j, t) | w _j <0 }. Затем они определяют емкости дуги c _si = w _i, если w _i > 0, и c _jt = −w _j, если w _j <0. Затем мы имеем

Для S ⊆ V {s} ∪ S является исходным набором минимального сечения в G _st = (V ', A') тогда и только тогда, когда (S, V \ S) является максимальным срезом блокировки в графе G.

Последняя проблема может быть легко решена с помощью алгоритма максимального потока, используя теорему о максимальном потоке. Фактически вы можете использовать задание 1 в качестве источника, поскольку оно гарантированно является частью набора источников (заданий, выполняемых на старой машине).