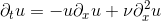Регулировка вязкости с помощью решателей оды scipy

Question

Рассмотрим для простоты следующее уравнение (уравнение Бюргерса):

Давайте решим это с помощью scipy (в моем случае scipy.integrate.ode.set_integrator("zvode", ..).integrate(T)) с помощью решателя с переменным шагом по времени.

Проблема в следующем: если мы используем наивную реализацию в пространстве Фурье

тогда член вязкости nu * d2x(u[t])может вызвать перерегулирование, если временной шаг слишком велик. Это может привести к изрядному количеству шума в решениях или даже к (поддельным) расходящимся решениям (даже с жесткими решателями в немного более сложной версии этого уравнения).

Один из способов упорядочить это - оценить член вязкости на этапеt+dt, и шаг обновления становится

Это решение хорошо работает при явном программировании. Как я могу использовать scipy для его реализации с переменным шагом? К моему удивлению, я не нашел никакой документации по этому довольно элементарному, сложному вопросу...

Answer 1

На самом деле вы не можете, или, наоборот, odeint или ode->zvode уже делает это для любой данной проблемы.

Для первого вам нужно будет указать две части уравнения отдельно. Очевидно, это не часть интерфейса решателя. Посмотрите на решатели DDE и SDE, где действительно требуется такое разбиение уравнения.

Ко второму, odeint а также ode->zvode использовать неявные многошаговые методы, что означает, что значения u(t+dt) а правая часть вводит вычисление и лежащее в основе локальное приближение.

Вы все равно можете попытаться внедрить свой исходный подход в решатель, предоставив функцию Якоби, которая содержит только второй член производной, но вполне вероятно, что вы не добьетесь улучшения.

Вы можете разбить ОДУ на разделы и решить линейную часть отдельно, введя

vhat(k,t) = exp(nu*k^2*t)*uhat(k,t)

так что

d/dt vhat(k,t) = -i*k*exp(nu*k^2*t)*conv(uhat(.,t),uhat(.,t))(k)