Решить систему линейных уравнений и линейных неравенств

Question

Я должен получить min и max y для линейного выражения, ограниченного некоторыми линейными неравенствами в python.

Здесь вы можете увидеть уравнения и неравенства, которые я ввел в Desmos:

3x+12y = 1000
x > 30
x < 160
y < 60
y > 10
x + y > 180

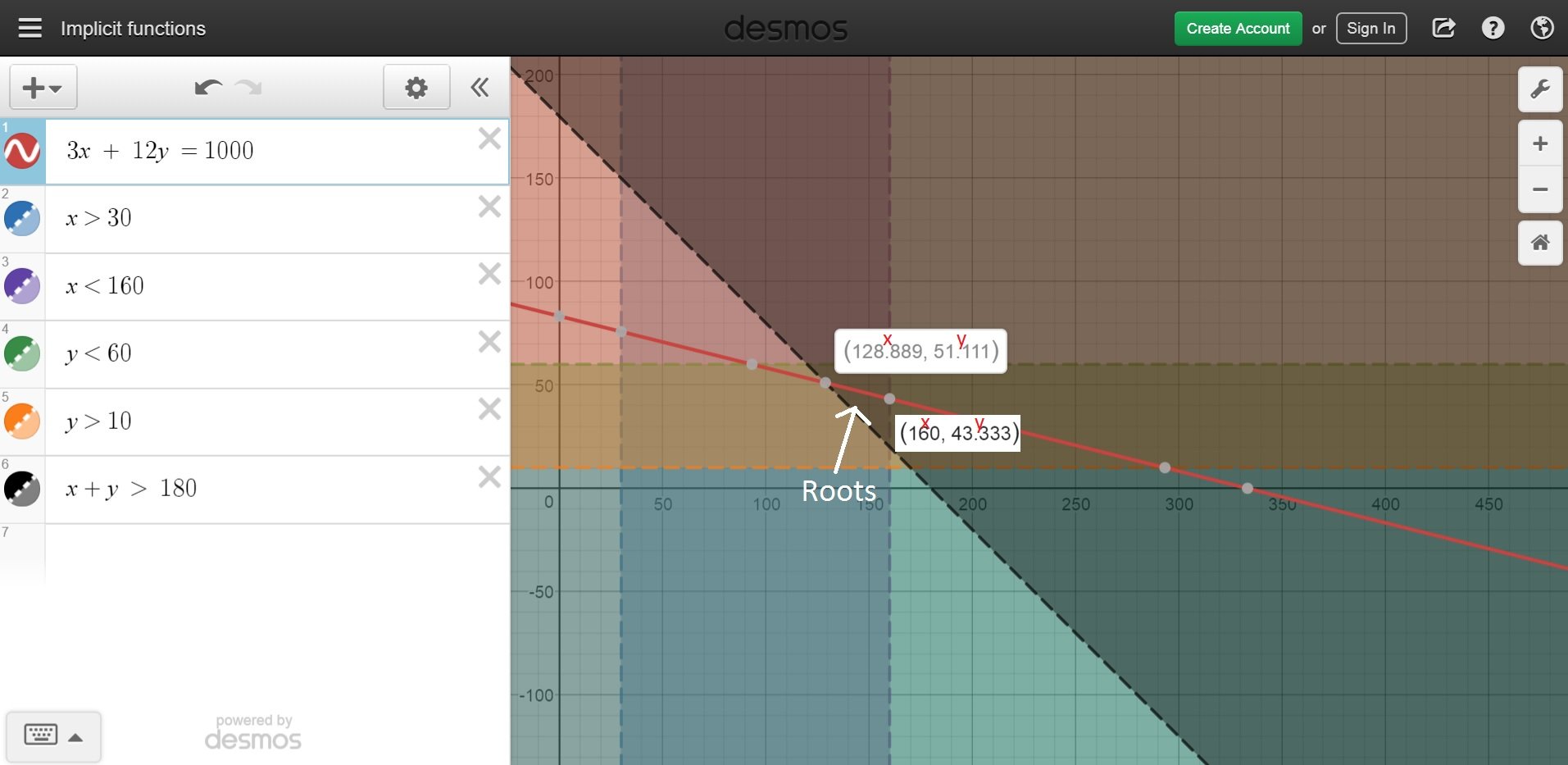
Я могу решить их вручную, нарисовав и вычеркнув неравенства. Но я не могу сделать это в Python. В Python я до сих пор пытался получить y=83,33 при x=0; х =333,33 при у = 0; После получения min и max x,y я затем применяю неравенства 1 на 1. Но к каждому неравенству я должен добавить предыдущие, а также проверить, прошел ли x или y определенный диапазон и пока он почти равен уверен, что я пропущу проверку.

Я посмотрел на numpy и sympy, но не мог понять, как решить это, используя их. Можете ли вы предложить, что / как я могу использовать, чтобы получить диапазон, который белая стрелка показывает на картинке?

Answer 1

Ваша проблема в линейном программировании, где ваши равенства и неравенства являются ограничениями, и вы хотите минимизировать (а затем и максимизировать) выражение y, Равенство, неравенства и выражения являются линейными, что делает его линейным программированием. scipy пакет, используя scipy.optimize.linprog функция, может сделать этот вид линейного программирования.

Вот закомментированный код, чтобы делать то, что вы хотите. Обратите внимание, что все неравенства были немного изменены, чтобы включить равенство, которое необходимо иметь максимальное или минимальное значение y, Чтобы найти максимальное значение y вместо этого код находит минимальное значение -y затем печатает аддитивную обратную, так как linprog минимизирует целевую функцию. Наконец, ограничения неравенства должны быть "меньше или равны" в linprogпоэтому я умножил обе стороны вашего неравенства x + y > 180 от -1 чтобы получить один, а именно -x + -y <= -180, Спросите, если у вас есть какие-либо вопросы.

from scipy.optimize import linprog

# Set up values relating to both minimum and maximum values of y
coefficients_inequalities = [[-1, -1]]  # require -1*x + -1*y <= -180
constants_inequalities = [-180]
coefficients_equalities = [[3, 12]]  # require 3*x + 12*y = 1000
constants_equalities = [1000]
bounds_x = (30, 160)  # require 30 <= x <= 160
bounds_y = (10, 60)  # require 10 <= y <= 60

# Find and print the minimal value of y
coefficients_min_y = [0, 1]  # minimize 0*x + 1*y
res = linprog(coefficients_min_y,
              A_ub=coefficients_inequalities,
              b_ub=constants_inequalities,
              A_eq=coefficients_equalities,
              b_eq=constants_equalities,
              bounds=(bounds_x, bounds_y))
print('Minimum value of y =', res.fun)

# Find and print the maximal value of y = minimal value of -y
coefficients_max_y = [0, -1]  # minimize 0*x + -1*y
res = linprog(coefficients_max_y,
              A_ub=coefficients_inequalities,
              b_ub=constants_inequalities,
              A_eq=coefficients_equalities,
              b_eq=constants_equalities,
              bounds=(bounds_x, bounds_y))
print('Maximum value of y =', -res.fun)  # opposite of value of -y

Распечатка из этого кода

Minimum value of y = 43.3333333333
Maximum value of y = 51.1111111111

что правильно с точностью до плавающей запятой. Если вам нужны соответствующие значения xсм значение res.x который является массивом, который дает значения обоих x а также y в нужной точке--x является res.x[0] а также y является res.x[1],

Answer 2

Следуя подсказке, приведенной в комментарии, вы можете решить вашу проблему, используя scipy.optimize.linprog следующим образом...

In [1]: import numpy as np

In [2]: from scipy import optimize

In [3]: c = np.zeros(2)

In [4]: A_ub = np.array([[-1, -1]])

In [5]: b_ub = np.array([-180])

In [6]: A_eq = np.array([[3, 12]])

In [7]: b_eq = np.array([1000])

In [8]: bounds = [(30, 160), (10, 60)]

In [9]: optimize.linprog(c, A_ub, b_ub, A_eq, b_eq, bounds, method="simplex")
Out[11]: 
     fun: -0.0
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([ 31.11111111,  98.88888889,   0.        ,  41.11111111,   8.88888889])
  status: 0
 success: True
       x: array([ 128.88888889,   51.11111111])

Хитрость заключается в том, чтобы отметить, что решение системы уравнений может быть выражено как задача оптимизации с постоянной нулевой целевой функцией. Вот почему я установил c=np.zeros(2) выше.

Answer 3

Вы можете попробовать cvxpy. Это решение для выпуклых задач, поэтому оно может быть излишним для ваших нужд. Мне нравится, как легко закодировать вашу проблему с ним. Большинство других библиотек требуют, чтобы вы закодировали свою проблему в несколько матриц.