Аппаратные образцы из подобранного гауссовского процесса не похожи на предсказанное среднее

Question

Я подбираю гауссовский процесс на основе второго графика, показанного здесь, и беру из него образцы. Однако нарисованные выборки не похожи на подобранную функцию и, как правило, сильно отличаются от предсказанного среднего (в частности, они не такие гладкие и имеют резкие изменения) и не проходят (или близко) к заданным точкам данных (красный точек на сюжете).

Пример графика (черная линия - это прогнозируемое среднее, синяя и оранжевая линии - образцы):

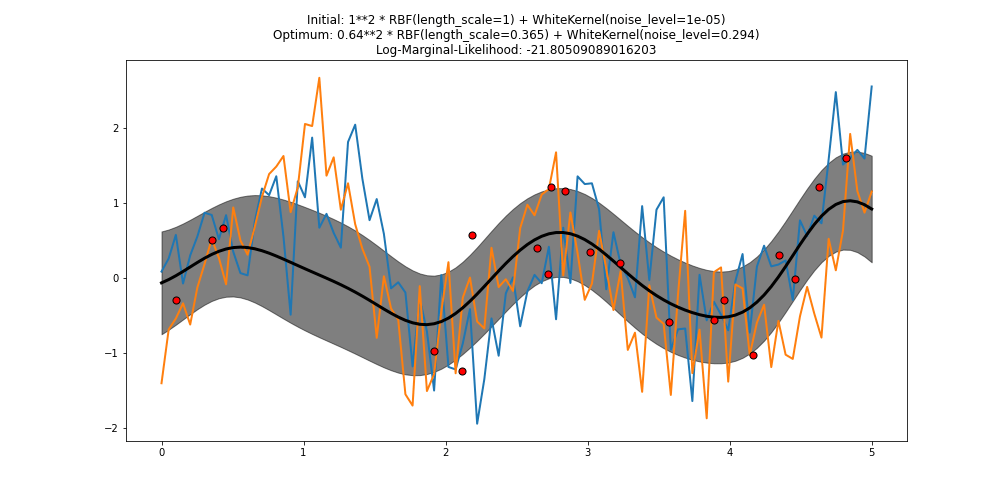
После многих прогонов результат всегда будет одинаковым (даже если не совсем таким). Есть идеи, что вызывает это и как я могу сделать нарисованные образцы более похожими на среднее значение?

Код, используемый для создания графика:

import numpy as np

from matplotlib import pyplot as plt

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel as White


rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 20)[:, np.newaxis]
y = 0.5 * np.sin(3 * X[:, 0]) + rng.normal(0, 0.5, X.shape[0])

kernel = 1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e3)) \
    + White(noise_level=1e-5, noise_level_bounds=(1e-10, 1e+1))
gp = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gp.fit(X, y)

X_ = np.linspace(0, 5, 100)
y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)

plt.figure(figsize=(14,7))
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - np.sqrt(np.diag(y_cov)),
                 y_mean + np.sqrt(np.diag(y_cov)),
                 alpha=0.5, color='k')
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.title("Initial: %s\nOptimum: %s\nLog-Marginal-Likelihood: %s"
          % (kernel, gp.kernel_, gp.log_marginal_likelihood(gp.kernel_.theta)))
y_samples = gp.sample_y(X_.reshape(-1, 1), 2)
plt.plot(X_, y_samples, lw=2)
plt.tight_layout()

Answer 1

Недавно я изучаю процесс терапевта и пытаюсь дать интуитивное объяснение :

Задний план:

Истинная (игрушечная) функция для изучения - это синусоидальная функция: (0,5 * синус x) + корректировка нормального распределения (среднее значение =0, стандартное отклонение =0,5)

Регрессор гауссовского процесса пытается учиться и соответствовать (на основе некоторых заданных обучающих пар (X, y) / априорное распределение) и последовательно прийти к некоторому апостериорному распределению. Чем больше очков обучения дается, тем лучше качество прогноза.

Текущий код и демонстрация

Регрессор GP попытается дать прогнозируемое среднее значение + доверительный диапазон (например, одна SD в данном случае). В случае данной функции, связанной с синусом, ее истинная форма обычно похожа на красную линию с учетом моего третьего приложения (обратите внимание, что красная линия, построенная из 100 контрольных точек, временами может сильно отличаться от других, частично из-за случайной нормальной настройки на уравнение синуса.

Я прилагаю еще три случая: i) 80 предыдущих точек обучения и ii) 10 предыдущих точек обучения, iii) с графиком истинной апостериорной функции для 100 X входных данных для сравнения с текущим случаем из 20 точек (пожалуйста, обратите внимание, что график из 10 точек обучения показывает переоборудование в одном регионе и недостаточное в других)

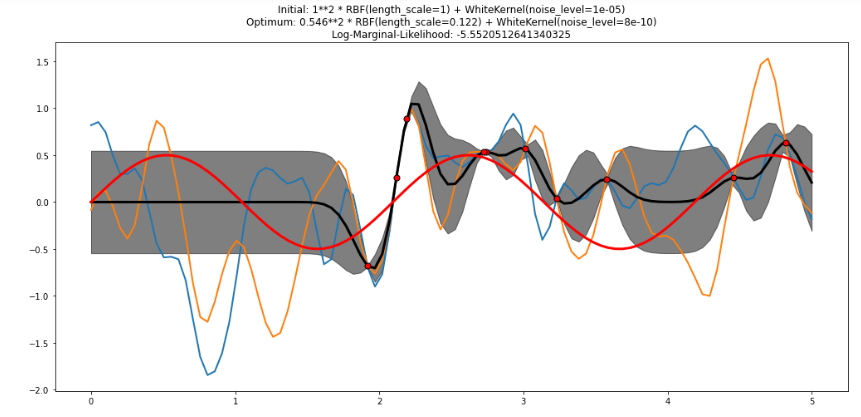[ Чего нам следует ожидать от образца, предоставленного gp.sample_y?

В нашем прогнозе в основном следует руководствоваться прогнозируемым средним (черный) и уровнем достоверности (серый). То, что вы пробуете из sample_y, является "одной из многих" реализаций процесса. Интуитивно это похоже на то, как если бы вы бросали кости из N граней в течение периода времени T, и, поскольку вы можете дополнительно разделить T и подразделить N, это становится бесконечной комбинацией. Даже если мы сохраняем диапазон и все целые числа, это все равно огромная комбинация возможных подраспределений (выборок).

Таким образом, независимо от того, в предшествующем или апостериорном распределении: i) эти выборки точно НЕ такие гладкие, как совокупность (как и любые отдельные игры); и ii) многие из них ведут себя по-разному, но iii) в совокупности они образуют определенные Гауссов узор.

В моем ограниченном понимании выборка - это всего лишь возможное происшествие из многих, и большую часть времени результат находится в пределах или близко к диапазону достоверности, и прогноз обычно основывается на прогнозируемом среднем значении (черная линия)

Ссылка: https://peterroelants.github.io/posts/gaussian-process-tutorial/