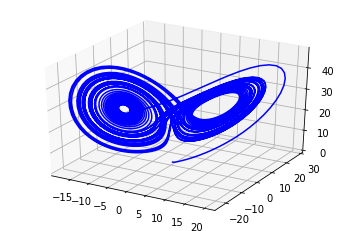
Аттрактор Лоренца с питоном Рунге-Кутта

  1. Здравствуйте, мне нужно запрограммировать функцию Python для решения дифференциальных уравнений Лоренца с использованием 2-го класса Рунге-Кутта

Дифференциальное уравнение

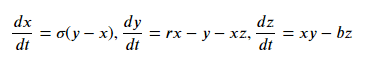
сигма =10, r=28 и b=8/3

с начальными условиями (x,y,z)=(0,1,0)

это код, который я написал, но он выдает ошибку, говоря, что в double_scalars, и я не вижу, что не так с программой

from pylab import *
def runge_4(r0,a,b,n,f1,f2,f3):
    def f(r,t):
        x=r[0]
        y=r[1]
        z=r[2]
        fx=f1(x,y,z,t)
        fy=f2(x,y,z,t)
        fz=f3(x,y,z,t)
        return array([fx,fy,fz],float)
    h=(b-a)/n
    lista_t=arange(a,b,h)
    print(lista_t)
    X,Y,Z=[],[],[]
    for t in lista_t:
        k1=h*f(r0,t)
        print("k1=",k1)
        k2=h*f(r0+0.5*k1,t+0.5*h)
        print("k2=",k2)
        k3=h*f(r0+0.5*k2,t+0.5*h)
        print("k3=",k3)
        k4=h*f(r0+k3,t+h)
        print("k4=",k4)
        r0+=(k1+2*k2+2*k3+k4)/float(6)
        print(r0)
        X.append(r0[0])
        Y.append(r0[1])
        Z.append(r0[2])
    return array([X,Y,Z])

def f1(x,y,z,t):
    return 10*(y-x)
def f2(x,y,z,t):
    return 28*x-y-x*z
def f3(x,y,z,t):
    return x*y-(8.0/3.0)*z
#and I run it
r0=[1,1,1]

runge_4(r0,1,50,20,f1,f2,f3)
Источник

3 ответа

Решение

Численное решение дифференциальных уравнений может оказаться сложной задачей. Если вы выберете слишком большие размеры шага, решение будет накапливать большое количество ошибок и даже может стать нестабильным, как в вашем случае.

Либо вам следует резко уменьшить размер шага (h) или просто воспользуйтесь адаптивным методом Рунге Кутта, предоставленным scipy:

from numpy import array, linspace
from scipy.integrate import solve_ivp
import pylab
from mpl_toolkits import mplot3d

def func(t, r):
    x, y, z = r 
    fx = 10 * (y - x)
    fy = 28 * x - y - x * z
    fz = x * y - (8.0 / 3.0) * z
    return array([fx, fy, fz], float)

# and I run it
r0 = [0, 1, 0]
sol = solve_ivp(func, [0, 50], r0, t_eval=linspace(0, 50, 5000))

# and plot it
fig = pylab.figure()
ax = pylab.axes(projection="3d")
ax.plot3D(sol.y[0,:], sol.y[1,:], sol.y[2,:], 'blue')
pylab.show()

Этот решатель использует комбинацию Рунге-Кутты 4-го и 5-го порядков и контролирует отклонение между ними, изменяя размер шага. См. Дополнительную документацию по использованию здесь: https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html

Источник

Вы используете размер шага h=2.5.

Для RK4 полезные размеры шага с учетом константы Липшица L находятся в диапазоне L*h=1e-3 к 0.1, можно получить несколько правильные результаты до L*h=2.5. Помимо этого, метод становится хаотичным, теряется всякое сходство с лежащим в его основе ODE.

В системе Лоренца постоянная Липшица составляет около L=50см. Хаос и непрерывная зависимость решения ODE, поэтомуh<0.05 абсолютно необходимо, h=0.002 лучше и h=2e-5 дает наилучшие численные результаты для этого численного метода.

Источник

Это может быть связано с делением на ноль или превышением ограничения типа (тип с плавающей запятой).

Чтобы выяснить, где и когда это произойдет, вы можете установить numpy.seterr('raise')и это вызовет исключение, чтобы вы могли отладить и увидеть, что происходит. Похоже, ваш алгоритм расходится.

Здесь вы можете увидеть, как использовать numpy.seterr

Источник
Другие вопросы по тегам