Как найти обратное для метода обратной выборки в R

Question

Как правило, для метода обратной выборки у нас есть плотность, и мы хотели бы использовать ее. Первый шаг - найти кумулятивную функцию плотности для плотности. Затем найти обратную функцию и, наконец, найти обратную функцию для случайно выбранного значения из равномерного распределения.

Например, у меня есть такая функция y= ((3/2)/(1+x)^2) поэтому cdf равен (3x)/2(x+1) а обратный к cdf равен ((3/2)*u)/(1-(3/2)*u)

Для этого в R я написал

 f<-function(x){
 y= ((3/2)/(1+x)^2)
 return(y)
}



cdf <- function(x){
  integrate(f, -Inf, x)$value
}

invcdf <- function(q){
  uniroot(function(x){cdf(x) - q}, range(x))$root
}
U <- runif(1e6)
X <- invcdf(U)

У меня две проблемы! Во-первых: код возвращает функцию, а не образцы. Второй: есть ли другой простой способ сделать эту работу? например, чтобы найти cdf и инверсию более простыми способами?

Хочу добавить, что я не ищу эффективности кода. Меня просто интересует код, который мог бы написать новичок.

Answer 1

Вы можете попробовать численный подход к обратной выборке. По вашему запросу, это больше о прозрачности метода, чем об эффективности.

Эта функция будет численно интегрировать заданную функцию в заданном диапазоне (хотя она будет обрезать бесконечные значения)

cdf <- function(f, lower_bound, upper_bound)
{
  if(lower_bound < -10000) lower_bound <- -10000          # Trim large negatives
  if(upper_bound > 10000) upper_bound <- 10000            # Trim large positive
  x <- seq(lower_bound, upper_bound, length.out = 100001) # Finely divide x axis
  delta <- mean(diff(x))                                  # Get delta x (i.e. dx)
  mid_x <- (x[-1] + x[-length(x)])/2                      # Get the mid point of each slice
  result <- cumsum(delta * f(mid_x))                      # sum f(x) dx
  result <- result / max(result)                          # normalize
  list(x = mid_x, cdf = result)                           # return both x and f(x) in list
}

И чтобы получить обратное, мы находим ближайшее значение в cdf случайного числа, взятого из равномерного распределения между 0 и 1. Затем мы видим, какое значение x соответствует этому значению cdf. Мы хотим иметь возможность делать это для n образцов за раз, поэтому мы используемsapply:

inverse_sample <- function(f, n = 1, lower_bound = -1000, upper_bound = 1000)
{
  CDF <- cdf(f, lower_bound, upper_bound)
  samples <- runif(n)
  sapply(samples, function(s) CDF$x[which.min(abs(s - CDF$cdf))])
}

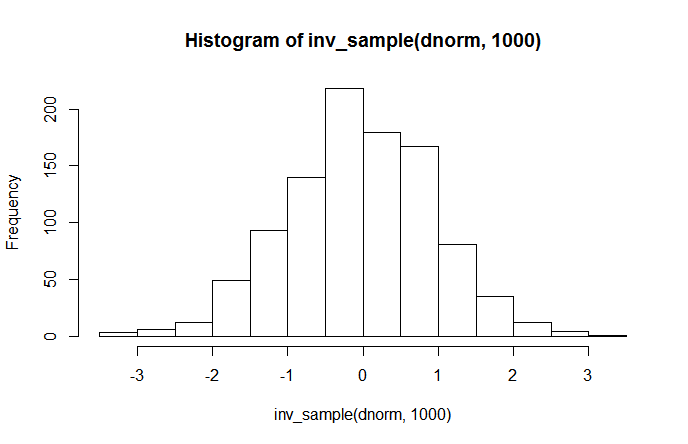
Мы можем проверить это, нарисовав гистограммы результатов. Начнем с функции плотности нормального распределения (dnorm в R), вычерчивая 1000 выборок и нанося на график их распределение:

hist(inv_sample(dnorm, 1000))

И мы можем сделать то же самое для экспоненциального распределения, на этот раз установив пределы интегрирования от 0 до 100:

hist(inv_sample(dexp, 1000, 0, 100))

И, наконец, мы можем сделать то же самое на вашем собственном примере:

f <- function(x) 3/2/(1 + x)^2

hist(inv_sample(f, 1000, 0, 10))