Есть ли способ построить непрерывную линию с наклоном, вычисленным по парам координат?
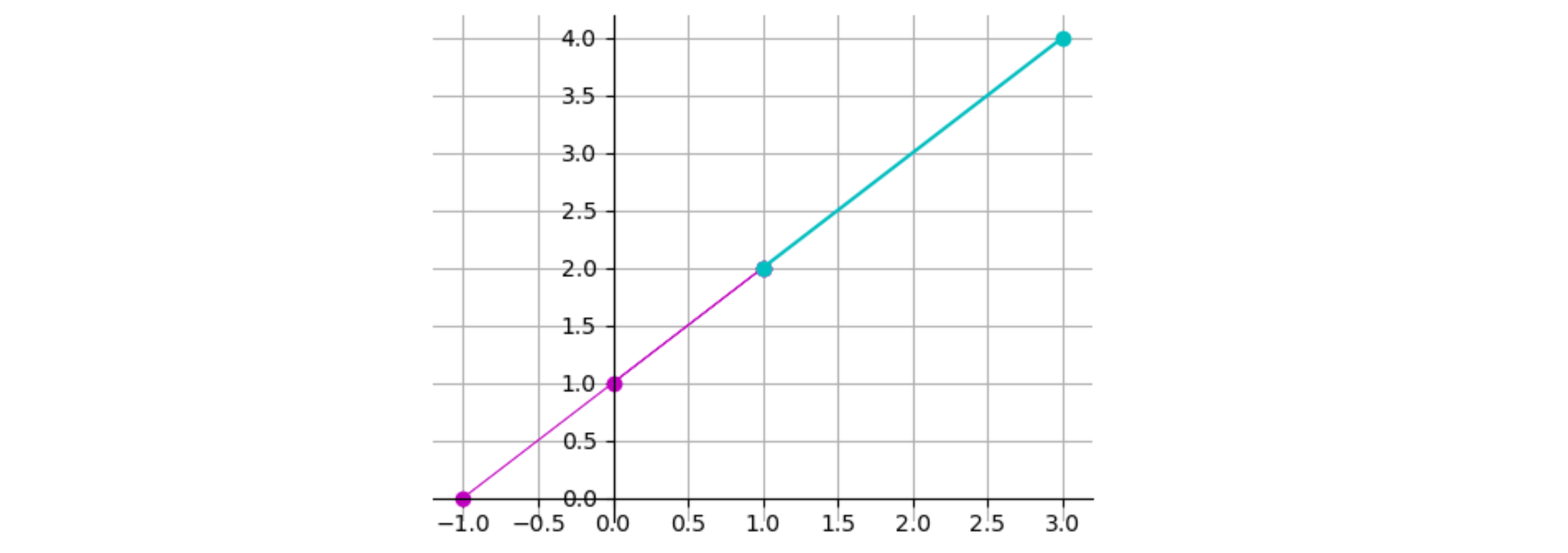
Я новичок в кодировании, и в настоящее время я работаю над созданием программы, которая вычисляет форму пересечения наклона линии и такую информацию, как пересечение по оси x и точку пересечения по оси y этой линии, исходя из значений любых двух случайных пар координат для пример (x1,y1), (x2,y2) = (1,2), (3,4) то, что это представляет, как в matplotlib, при построении представляет собой отрезок линии с вычисленным наклоном (здесь оказывается 1 y = 1x + 1), не пересекающий ни одну ось ". Я хотел бы провести над ним еще одну линию с тем же наклоном, что и непрерывный сегмент линии, чтобы показать, где сегмент линии будет пересекать оси x и y, но я хочу сделать это для любой комбинации ввода случайных пар координат. пользователем. Я также хотел бы настроить загрузку графика с началом координат графика (0,0) в левом нижнем углу кадра, когда он создается, и не иметь графика, центрированного вокруг моего линейного сегмента, когда он создается. Буду признателен за любую оказанную помощь.
import numpy as np
import math
x1 = float(input("Enter a x coordinate for x1: "))
y1 = float(input("Enter a y coordinate for y1: "))
x2 = float(input("Enter a x coordinate for x2: "))
y2 = float(input("Enter a y coordinate for y2: "))
m = (y2-y1)/(x2-x1)
d = math.sqrt((x2 - x1)**2 + (y2-y1)**2)
slope_multiplied_by_negative_x1 = m * (-1 * x1)
b = float(y1) + float(slope_multiplied_by_negative_x1)
b_absolute = abs(b)
result = "y = " + (str(m) + "x " if m != 0 else "")
if m == 0:
sign = ""
elif b == 0:
sign = ""
elif b > 0:
sign = "+ "
else:
sign = "- "
try: X_intercept = float((-1 * b)/m)
except ZeroDivisionError:
X_intercept = 'n/a'
print(result + sign + ("" if b == 0 else (str(b_absolute))))
print("X intercept: " + ("0.0" if X_intercept == 0 else str(X_intercept)))
print("Y intercept: " + str(b))
print("Distance between (x1,y1) and (x2,y2): " + str(d))
x = [x1,x2]
y=[y1,y2]
t = np.arange(0.0, 2.0, 0.01)
fig, ax = plt.subplots()
plt.plot(x, y, color='c', linestyle='-', marker='o')
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.grid()
plt.show()
2 ответа
Сегмент с конечными точками (x1,y1), (x2,y2) принадлежит линии с уравнением
(x - x1) / (x2 - x1) = (y - y1) / (y2 - y1)
Сначала нам нужно проверить дополнительные случаи вертикальных и горизонтальных линий:
if x1 == x2:
x_intercept = x1
y_intercept does not exist
use screen window border coordinates to draw line
(x1,0)-(x1,height)
if y1 == y2:
y_intercept = y1
x_intercept does not exist
use screen window border coordinates to draw line
(0,y1)-(width,y1)
В противном случае, чтобы найти пересечения с осями, мы можем просто подставить y=0 или x=0 к этому уравнению.
x_intercept = x1 - y1 * (x2 - x1) / (y2 - y1)
y_intercept = y1 - x1 * (y2 - y1) / (x2 - x1)
draw line
(0, y_intercept) - (x_intercept, 0)
PS Обратите внимание, что вам редко требуется наклон в вычислительной геометрии - существует множество более общих подходов для определения линии (описанный один, параметрический метод, метод тета-ро)
Вот подход, не меняющий слишком сильно исходный код. Он проверяет наличие горизонтальных и вертикальных линий и дает результат, когда начальная и конечная точки равны.
Точка (0,0) принудительно помещается на график, рисуя там невидимую точку. Линии добавляются между каждой конечной точкой и каждым перехватом. Это также приведет к тому, что оба (если они существуют) будут в области построения. Вы заметите, что при этом одни и те же сегменты будут отрисовываться несколько раз, но при этом не будет слишком много тестов, чтобы знать, какие сегменты необходимы. Порядок рисования гарантирует, что сегмент между (x1,y1) и (x2,y2) находится наверху.
Numpy удален, так как здесь он не нужен, но был бы полезен для других типов кривых. Преобразование в числа с плавающей запятой обычно не требуется в вычислениях, поскольку Python3 автоматически преобразует целые числа в числа с плавающей запятой для делений.
Некоторые расширения, которые можно было бы рассмотреть:
- проверка числа с плавающей запятой на равенство во избежание деления на 0 может быть опасной для числа с плавающей запятой в результате больших вычислений; иногда числа с плавающей запятой почти, но не точно, равны, и деление на их разность приводит к переполнению (или нежелательным большим числам)
- чтобы удлинить линии до тех пор, пока они не коснутся границ, вам нужно будет решить уравнения, чтобы найти пересечения с каждой из четырех границ и отклонить те пересечения, которые выходят за пределы других границ
- в качестве альтернативы вы можете нарисовать очень длинную линию и затем повторно применить ограничения x и y
Вот код, который может послужить базой для дальнейших экспериментов:
import matplotlib.pyplot as plt
import math
x1 = float(input("Enter a x coordinate for x1: "))
y1 = float(input("Enter a y coordinate for y1: "))
x2 = float(input("Enter a x coordinate for x2: "))
y2 = float(input("Enter a y coordinate for y2: "))
d = math.sqrt((x2 - x1)**2 + (y2-y1)**2)
if x2 != x1:
m = (y2-y1)/(x2-x1)
slope_multiplied_by_negative_x1 = m * (- x1)
b = y1 + slope_multiplied_by_negative_x1
result = "y = " + (str(m) + "x" if m != 0 else "")
if m != 0:
X_intercept = (-1 * b) / m
else:
X_intercept = 'n/a'
if m == 0:
sign = ""
elif b < 0:
sign = " - "
else:
sign = " + "
result = result + ("" if b == 0 else sign + str(abs(b)))
elif y1 != y2:
result = "x = " + str(x1)
X_intercept = x1
b = 'n/a'
else:
result = "(x, y) = (" + str(x1) + ", " + str(y1) + ')'
X_intercept = 'n/a' if x1 != 0 else x1
b = 'n/a' if y1 != 0 else y1
print(result)
print("X intercept: " + ("0.0" if X_intercept == 0 else str(X_intercept)))
print("Y intercept: " + str(b))
print("Distance between (x1,y1) and (x2,y2): " + str(d))
fig, ax = plt.subplots()
plt.plot(0, 0, color='k', marker='') # just to make sure the plot contains 0,0
if X_intercept != 'n/a':
plt.plot([X_intercept, x1], [0, y1], color='m', marker='o', linewidth=0.5)
plt.plot([X_intercept, x2], [0, y2], color='m', marker='', linewidth=0.5)
if b != 'n/a':
plt.plot([0, x1], [b, y1], color='m', marker='o', linewidth=0.5)
plt.plot([0, x2], [b, y2], color='m', marker='', linewidth=0.5)
plt.plot([x1, x2], [y1, y2], color='c', linestyle='-', marker='o')
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid()
plt.show()
Вот способ провести длинную линию. zorder=-1используется для принудительного размещения этой линии за другими линиями и точками. Мы называем это в конце (непосредственно передplt.show), поэтому matplotlib может автоматически рассчитать пределы, чтобы соответствовать всем предыдущим материалам.
xlims = plt.xlim() # save the current limits
ylims = plt.ylim()
dx = (x2 - x1) * 100
dy = (y2 - y1) * 100
plt.plot([x1 - dx, x2 + dx], [y1 - dy, y2 + dy], color='k', linestyle='-', marker='', linewidth=0.5, zorder=-1)
plt.xlim(xlims) # reapply the limits
plt.ylim(ylims)