NaN по матричной факторизации
Я реализовал матричную факторизацию с использованием алгоритма SGD, но я часто получаю NaN в прогнозируемой матрице, когда запускаю ее. Когда я запускаю алгоритм на очень маленькой (6 x 7) матрице, ошибка появляется мало раз. Поскольку я перешел к набору данных Movie Lens, я получаю сообщение об ошибке во всех ячейках каждый раз, когда запускаю алгоритм. Единственный раз, когда ошибка исчезает только в некоторых ячейках, - это когда я устанавливаю шаги оптимизации (количество итераций) на 1.
private static Matrix matrixFactorizationLarge (Matrix realRatingMatrix, Matrix factor_1, Matrix factor_2)
{
int features = (int) factor_1.getColumnCount();
double learningRate = 0.02;
double regularization = 0.02;
int optimizationSteps = 10;
Matrix predictedRatingMatrix = SparseMatrix.Factory.zeros(realRatingMatrix.getRowCount(), realRatingMatrix.getColumnCount());
for (int step = 0; step < optimizationSteps; step++)
{
for (int row = 0; row < predictedRatingMatrix.getRowCount(); row++)
{
for (int col = 0; col < predictedRatingMatrix.getColumnCount(); col++)
{
if (realRatingMatrix.getAsInt(row, col) > 0)
{
Matrix vector_1 = getRow(factor_1, row);
Matrix vector_2 = getColumn(factor_2, col);
predictedRatingMatrix.setAsDouble( ( Math.floor ( dotProduct(vector_1, vector_2) * 100 ) ) / 100, row, col);
for (int f = 0; f < features; f++)
{
factor_1.setAsDouble( ( Math.floor ( ( factor_1.getAsDouble(row, f) + ( learningRate * ( ( calculateDerivative(realRatingMatrix.getAsDouble(row, col), predictedRatingMatrix.getAsDouble(row, col), factor_2.getAsDouble(f, col) ) ) - ( regularization * factor_1.getAsDouble(row, f) ) ) ) ) * 100 ) / 100), row, f);
factor_2.setAsDouble( ( Math.floor ( ( factor_2.getAsDouble(f, col) + ( learningRate * ( ( calculateDerivative(realRatingMatrix.getAsDouble(row, col), predictedRatingMatrix.getAsDouble(row, col), factor_1.getAsDouble(row, f) ) ) - ( regularization * factor_2.getAsDouble(f, col) ) ) ) ) * 100 ) / 100), f, col);
}
}
}
}
}
return predictedRatingMatrix;
}
Связанные методы следующие:
private static double dotProduct (Matrix vector_A, Matrix vector_B)
{
double dotProduct = 0.0;
for (int index = 0; index < vector_A.getColumnCount(); index++)
{
dotProduct = dotProduct + ( vector_A.getAsDouble(0, index) * vector_B.getAsDouble(0, index) );
}
return dotProduct;
}
private static double errorOfDotProduct (double original, double dotProduct)
{
double error = 0.0;
error = Math.pow( ( original - dotProduct ), 2 );
return error;
}
private static double calculateDerivative(double realValue, double predictedValue, double value)
{
return ( 2 * (realValue - predictedValue) * (value) );
}
private static double calculateRMSE (Matrix realRatingMatrix, Matrix predictedRatingMatrix)
{
double rmse = 0.0;
double summation = 0.0;
for (int row = 0; row < realRatingMatrix.getRowCount(); row++)
{
for (int col = 0; col < realRatingMatrix.getColumnCount(); col++)
{
if (realRatingMatrix.getAsDouble(row, col) != 0)
{
summation = summation + errorOfDotProduct(realRatingMatrix.getAsDouble(row, col), predictedRatingMatrix.getAsDouble(row, col));
}
}
}
rmse = Math.sqrt(summation);
return rmse;
}
private static Matrix csvToMatrixLarge (File csvFile)
{
Scanner inputStream;
Matrix realRatingMatrix = SparseMatrix.Factory.zeros(610, 17000);
// Matrix realRatingMatrix = SparseMatrix.Factory.zeros(6, 7);
try
{
inputStream = new Scanner(csvFile);
while (inputStream.hasNext()) {
String ln = inputStream.next();
String[] values = ln.split(",");
double rating = Double.parseDouble(values[2]);
int row = Integer.parseInt(values[0])-1;
int col = Integer.parseInt(values[1])-1;
if (col < 1000)
{
realRatingMatrix.setAsDouble(rating, row, col);
}
}
inputStream.close();
}
catch (FileNotFoundException e)
{
e.printStackTrace();
}
return realRatingMatrix;
}
private static Matrix createFactorLarge (long rows, long features)
{
Matrix factor = DenseMatrix.Factory.zeros(rows, features);
return factor;
}
private static void fillInMatrixLarge (Matrix matrix)
{
for (int row = 0; row < matrix.getRowCount() ; row++)
{
for (int col = 0; col < matrix.getColumnCount(); col++)
{
double random = ThreadLocalRandom.current().nextDouble(5.1);
matrix.setAsDouble( (Math.floor (random * 10 ) / 10), row, col);
}
}
// return matrix;
}
private static Matrix getRow (Matrix matrix, int rowOfIntresst)
{
Matrix row = Matrix.Factory.zeros(1, matrix.getColumnCount());
for (int col = 0; col < matrix.getColumnCount(); col++)
{
row.setAsDouble(matrix.getAsDouble(rowOfIntresst, col), 0, col);
}
return row;
}
private static Matrix getColumn (Matrix matrix, int colOfInteresst)
{
Matrix column = Matrix.Factory.zeros(1, matrix.getRowCount());
for (int index = 0; index < matrix.getRowCount(); index++)
{
column.setAsDouble(matrix.getAsDouble(index, colOfInteresst), 0, index); //column[row] = matrix[row][colOfInteresst];
}
return column;
}
Что вызывает ошибку, поскольку я не делю на ноль в алгоритме? И как я могу это решить?
PS Я использую пакет универсальной матричной библиотеки
1 ответ
Ключ к тому, чтобы избежать ошибки Not a Number - NaN при факторизации матрицы, - это выбрать правильную скорость обучения. Важно отметить, что правильная скорость обучения всегда определяется количеством итераций. Ниже приведен пример, поясняющий проблему:
No. Of Iterations: 3
Learning Rate: 0.02
Regularization Rate: 0.02
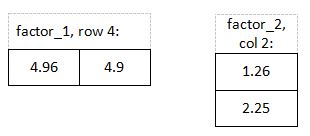
У нас есть следующие факторы в качестве примера на итерации 1 до оптимизации:
Прогнозируемый рейтинг, строка 4, столбец 2: ( 4,96 * 1,26) + ( 4,9 * 2,25) = 17,27
После оптимизации факторов мы получим:
Строка 4 и столбец 2 оптимизируются, пока мы не вернемся к ним на итерации 2:
Прогнозируемый рейтинг, строка 4, столбец 2: ( -2,31 * 233089,24) + ( -1,67 * -888,59) = -536952,2
Каждая ячейка в строке 4 и столбце 2 оптимизируется. Я покажу шаги оптимизации для строки 1, столбца 1:
-2.31 + 0.02 [ ( 2 ( 4 + 536952.2 ) ( 233089.24 ) ) - ( 0.02 * -2.31 ) ] =
-2.31 + 0.02 [ ( 2 * 536956.2 * 233089.24 ) - ( 0.02 * -2.31 ) ] =
-2.31 + 0.02 [ ( 250317425142.57 ) - ( 0.04 ) ] =
Как мы видим, на этом шаге мы получаем очень большое число для производной. Ключевым моментом здесь является выбор правильной скорости обучения. Скорость обучения определяет скорость приближения к минимуму. Если мы сделаем его слишком большим, мы можем пропустить минимум, перепрыгнув через него и уйдя в бесконечность.
-2.31 + 0.02 [ 250317425142,53 ] =
-2.31 + 5006348502,85 =
5006348500,54
По мере продолжения оптимизации мы получим Infinity для этой ячейки на следующей итерации, что приведет к ошибке NaN при добавлении числа.
Выбрав небольшую скорость обучения, мы избежим ошибки и быстро достигнем точки минимума.