Решение цепных реакций в прологе

Question

Одна из недавних задач, связанных с появлением кода, ставит перед мной задачу решить для наименьшего количества входного материала, который я могу использовать для применения заданного набора реакций и получения 1 единицы выходного материала.

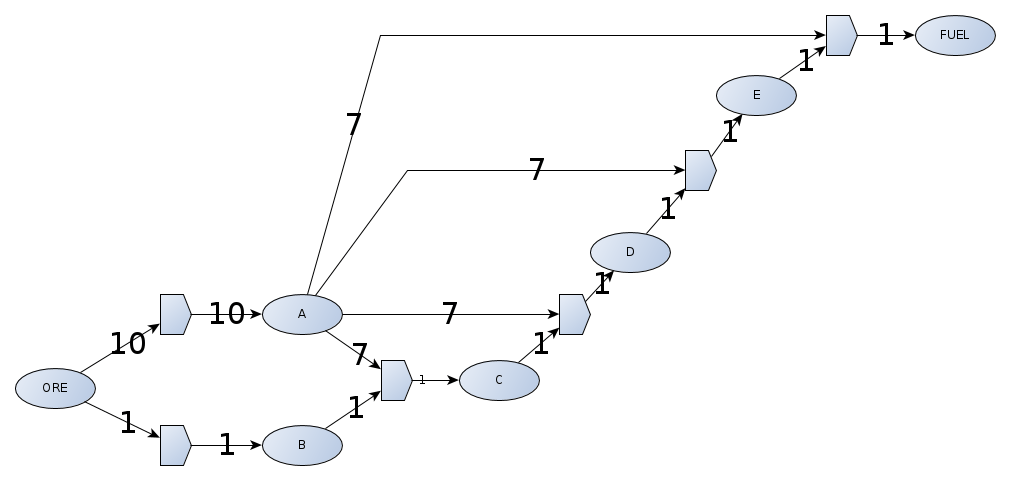
Например, учитывая

10 ORE => 10 A
1 ORE => 1 B
7 A, 1 B => 1 C
7 A, 1 C => 1 D
7 A, 1 D => 1 E
7 A, 1 E => 1 FUEL

Нам понадобится 31 руда, чтобы сделать 1 топливо (1 для производства единицы B, затем 30, чтобы получить необходимые 28 A).

В этом году я пытался расширить свой кругозор в языке программирования, поэтому я выполнил большинство задач в SML/NJ. Это кажется - казалось - подходящим для Prolog, учитывая то немногое, что я о нем знаю: логическое программирование, решение ограничений и т. Д.

Однако я не смог успешно смоделировать ограничения.

Я начал с того, что превратил этот простой пример в несколько фактов:

makes([ore(10)], a(10)).
makes([ore(1)], b(1)).
makes([a(7), b(7)], c(1)).
makes([a(7), c(1)], d(1)).
makes([a(7), d(1)], e(1)).
makes([a(7), e(1)], fuel(1)).

Если честно, я даже не уверен, является ли аргумент списка хорошей структурой или нотация функтора (ore(10)) тоже хорошая модель.

Затем я хотел создать правила, которые позволят вам сказать, например, что 10 руды достаточно для 7 а:

% handles the case where we have leftovers?
% is this even the right way to model all this... when we have leftovers, we may
% have to use them in the "reaction"...
makes(In, Out) :-
    Out =.. [F,N],
    Val #>= N,
    OutN =.. [F,Val],
    makes(In, OutN).

Это работает ¹, но я не уверен, что этого будет достаточно, поскольку мы можем заботиться об остатках (в конце концов, это проблема минимизации)?

Однако я застрял на следующих двух частях:

1. Я могу спросить, что дает 7 А и получить обратно 10 руд, но я не могу спросить, чего достаточно для 20 А: как мне написать правило, которое кодирует умножение / целочисленные множители?
2. Я могу сказать, что 7 A и 1 E составляют 1 топливо, но я не могу утверждать это рекурсивно: то есть я не могу утверждать, что 14 A и 1 D также дают 1 топливо. Как мне написать правило, которое это кодирует?

Я открыт для альтернативных кодировок данных для представленных мною фактов - в конечном итоге я буду писать сценарий преобразования входных данных Advent в факты Prolog, так что это меня меньше всего беспокоит. Я чувствую, что если мне удастся заставить этот небольшой пример работать, я смогу решить большую проблему.

---

1. ?- makes(X, a(7)). возвращает X=[ore(10)] бесконечно (т. е. если я продолжаю бить ;при появлении запроса он продолжает работать). Есть способ исправить это?

Answer 1

Это не прямой ответ на ваш конкретный вопрос, но моей первой мыслью об этой проблеме было использование chr в Prolog.

Затем я подумал, что перейду цепочку из fuel на сумму ore Мне нужно.

Основные ограничения:

:- chr_constraint ore/1, a/1, b/1,c/1, ab/1, bc/1, ca/1, fuel/0.

a(1),a(1) <=> ore(9).
b(1),b(1),b(1) <=> ore(8).
c(1),c(1),c(1),c(1),c(1) <=> ore(7).

ab(1) <=> a(3),b(4).
bc(1) <=> b(5),c(7).
ca(1) <=> c(4),a(1).
fuel <=> ab(2),bc(3),ca(4).

%Decompose foo/N into foo/1s

a(X) <=> X>1,Y#=X-1|a(Y),a(1).
b(X) <=> X>1,Y#=X-1|b(Y),b(1).
c(X) <=> X>1, Y#=X-1 | c(Y),c(1).

ab(X) <=> X>1, Y#=X-1|ab(Y),ab(1).
bc(X) <=> X>1,Y#=X-1| bc(Y),bc(1).
ca(X) <=> X>1, Y#= X-1| ca(Y),ca(1).

ore(X)<=>X >1, Y #= X -1 |ore(Y),ore(1).

%aggregation (for convenience) 
:- chr_constraint ore_add/1, total_ore/1.

total_ore(A), total_ore(Total) <=> NewTotal #= A + Total, total_ore(NewTotal).
ore_add(A) ==> total_ore(A).

ore(1) <=> ore_add(1).

Запрос:

?-fuel.
b(1),
b(1),
c(1),
c(1),
ore_add(1),
ore_add(1),
...
total_ore(150).

Затем вам нужно будет добавить процедуру поиска, чтобы исключить два b/1 и два c/1.

Я не реализовал это, но:

?-fuel,b(1),c(3).
ore_add(1),
...
total_ore(165)

Это только ore_add/1 ограничений и является правильным результатом.

Answer 2

Во время приготовления кофе это явно что-то для двигателя CLP(FD).

Если у нас есть ориентированный ациклический граф реакций с

• Узел ТОПЛИВО справа от графика и
• узлы для промежуточных продуктов IP[i] (i in 0..n) между ними, возможно
• несколько узлов ТОПЛИВА, т.е. несколько способов генерации ТОПЛИВА: ТОПЛИВО [0]... ТОПЛИВО [v] и, возможно,
• несколько узлов для промежуточных продуктов IP[i], т.е. несколько способов создания промежуточных продуктов IP [i> 0]: IP[i, 1]... IP[i, routes (i)] и
• IP [0] идентифицирован с ORE в левой части графика.

последние два пункта дают нам возможность выбрать стратегию для ассортимента продукции, тогда:

FUEL_NEEDED   = mix[0] * FUEL[0] + ... + mix[v] * FUEL[v]

со всем, что указано выше, переменная

и следующее, заданное в постановке задачи, с переменными FUEL[0]... FUEL[v] и остальными константами:

out_fuel[0] * FUEL[0] = ∑_j ( IP[j] * flow(IPj->FUEL0) )
⋮
out_fuel[v] * FUEL[v] = ∑_j ( IP[j] * flow(IPj->FUELv) )

и для каждого IP[i>0], с переменными IP[i] и остальными константами:

out_ip[i] * IP[i] = ∑_j≠i ( IP[j] * flow(IPj->IPi) )

в случае нескольких способов генерации IP[i] мы смешиваем (это похоже на введение узла графа для смеси IP[i] из его возможных способов IP[i, j]):

out_ip[i]   * IP[i]   = ∑_j(0..ways(i)) ( IP[i,j] * mix[i,j] )

out_ip[i,1] * IP[i,1] = ∑_j≠i ( IP[j] * flow(IP[j]->IP[i,1]) )
⋮
out_ip[i,ways(i)] * IP[i,ways(i)] = ∑_j≠i ( IP[j] * flow(IP[j]->IP[i,ways(i)]) )

а также IP[0] (т.е. ORE) свободная переменная, которую нужно минимизировать.

Здесь появляется недоопределенная проблема линейного программирования с матрицей, имеющей нули ниже диагонали, потому что это DAG, но она содержит переменные, которые необходимо оптимизировать в самой матрице. Как атаковать это?

Answer 3

В этом примере нет "альтернативного" пути и нет нескольких "источников руды", поэтому кодирование примера очень негибким способом с использованием Prolog можно выполнить следующим образом:

need(FUEL,OREOUT) :- need(FUEL,0,0,0,0,0,0,OREOUT).

need(FUEL,E,D,C,A,B,ORE,OREOUT) :- FUEL > 0, A2 is 7*FUEL+A, E2 is FUEL+E, need(0, E2, D, C, A2, B, ORE,OREOUT).
need(0,E,D,C,A,B,ORE,OREOUT)    :- E > 0, A2 is 7*E+A, D2 is E+D, need(0, 0, D2, C, A2, B, ORE,OREOUT).
need(0,0,D,C,A,B,ORE,OREOUT)    :- D > 0, A2 is 7*D+A, C2 is D+C, need(0, 0, 0, C2, A2, B, ORE,OREOUT).
need(0,0,0,C,A,B,ORE,OREOUT)    :- C > 0, A2 is 7*C+A, B2 is C+B, need(0, 0, 0, 0, A2, B2, ORE,OREOUT).
need(0,0,0,0,A,B,ORE,OREOUT)    :- X is A + B, X > 0, ORE2 is ORE + (A + 9)//10 + B, need(0, 0, 0, 0, 0, 0, ORE2,OREOUT).
need(0, 0, 0, 0, 0, 0, ORE, ORE).

затем

?- need(1011,ORE).
ORE = 3842

Но это просто глупая и неэлегантная попытка.

За этим скрывается главная общая проблема, которая включает в себя разбор произвольно сложного ациклического графа, ориентированного на реакцию, и построение соответствующей структуры. Хорошая идея состоит в том, что это DAG, поэтому нельзя создать "более ранний ингредиент" из "более позднего".